题目内容
12.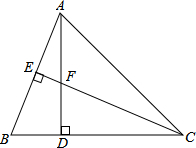 如图,在△ABC中,AD⊥BC于点D,AD=CD=2,过点C作CE⊥AB,交AD于点F,若BD=DF=2$\sqrt{2}$-2,CF=2BE,则AC的长为$2\sqrt{2}$.
如图,在△ABC中,AD⊥BC于点D,AD=CD=2,过点C作CE⊥AB,交AD于点F,若BD=DF=2$\sqrt{2}$-2,CF=2BE,则AC的长为$2\sqrt{2}$.
分析 因为AD⊥BC,所以△ADC为直角三角形,AD=CD=2,根据勾股定理,即可解答.
解答 解:∵AD⊥BC,
∴△ADC为直角三角形,
∵AD=CD=2,
根据勾股定理,得
$AC=\sqrt{A{D}^{2}+C{D}^{2}}=\sqrt{{2}^{2}+{2}^{2}}=\sqrt{8}=2\sqrt{2}$.
故答案为:$2\sqrt{2}$.
点评 本题考查了勾股定理,解决本题的关键是由AD⊥BC,得△ADC为直角三角形,运用勾股定理求出AC即可.

练习册系列答案
相关题目
12.可以来证明命题“若a2<0.04,则a<0.2”是假命题的反例( )
| A. | 可以是a=-0.2,不可以是a=-2 | |
| B. | 可以是a=-2,不可以是a=-0.2 | |
| C. | 可以是a=-0.2,也可以是a=-2 | |
| D. | 既不可以是a=-0.2,也不可以是a=-2 |
2.下列图案是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图所示,若四条直线两两相交于不同点,则图中有12对对顶角,有48对同位角,有24对内错角,有24对同旁内角.
如图所示,若四条直线两两相交于不同点,则图中有12对对顶角,有48对同位角,有24对内错角,有24对同旁内角.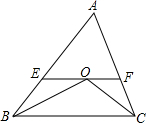 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5.
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5.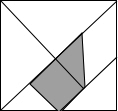 如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.
如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$. 如图所示,点A在点O的北偏东50°方向,点B在点O的南偏东10°方向上,则∠AOB=120°.
如图所示,点A在点O的北偏东50°方向,点B在点O的南偏东10°方向上,则∠AOB=120°.