题目内容
4.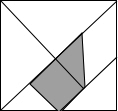 如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.
如图,是被称为“东方魔板”的七巧板,小明随意的向正方形内扎飞镖(线段的粗细忽略不计),则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$.
分析 根据一般说的七巧板,两个大三角形分别占大正方形的$\frac{1}{4}$,一个中三角形占正方形的$\frac{1}{8}$,一个正方形占正方形的$\frac{1}{8}$,一个平行四边形都是占正方形的$\frac{1}{8}$,两个小三角形分别占正方形的$\frac{1}{16}$,根据几何概率的定义求概率,即可解答.
解答 解:设正方形的面积为S,
∵一个正方形占正方形的$\frac{1}{8}$,小三角形占正方形的$\frac{1}{16}$,
∴阴影部分的面积为:($\frac{1}{8}+\frac{1}{16}$)S=$\frac{3}{16}$S,
∴则扎飞镖一次恰扎中阴影区域的概率为$\frac{3}{16}$S÷S=$\frac{3}{16}$.
故答案为:$\frac{3}{16}$.
点评 本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图图形中,阴影部分面积相等的是( )
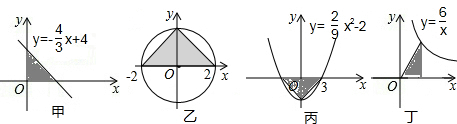

| A. | 甲乙 | B. | 甲丙 | C. | 乙丙 | D. | 丙丁 |
16. 如图,由B到A的方向是( )
如图,由B到A的方向是( )
 如图,由B到A的方向是( )
如图,由B到A的方向是( )| A. | 南偏东30° | B. | 东偏南60° | C. | 西偏北30° | D. | 北偏西60° |
14.下列说法正确的是( )
| A. | 0•a不是单项式 | B. | -$\frac{xyz}{3}$的系数是-$\frac{1}{3}$ | ||
| C. | -$\frac{abc}{4}$的系数是-4 | D. | x3y的系数是0 |
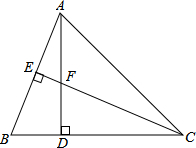 如图,在△ABC中,AD⊥BC于点D,AD=CD=2,过点C作CE⊥AB,交AD于点F,若BD=DF=2$\sqrt{2}$-2,CF=2BE,则AC的长为$2\sqrt{2}$.
如图,在△ABC中,AD⊥BC于点D,AD=CD=2,过点C作CE⊥AB,交AD于点F,若BD=DF=2$\sqrt{2}$-2,CF=2BE,则AC的长为$2\sqrt{2}$.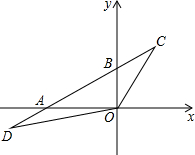 如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).
如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过点A(-4,0)、B(0,2)两点,点C、D在直线AB上,C的纵坐标为3,点D在第三象限,且△OBC与△OAD的面积相等,则点D的坐标为(-6,-1).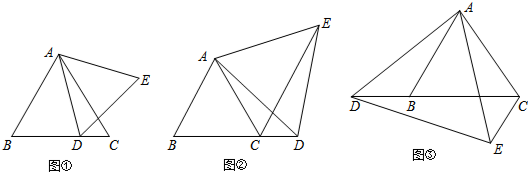
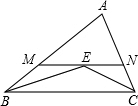 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=15,则线段MN的长为( )