题目内容
1.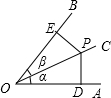 如图,设∠AOC=α,∠BOC=β,P为射线OC上一点,PD⊥OA于D,PE⊥OB于E,则$\frac{PD}{PE}$等于$\frac{sinα}{sinβ}$ (用α、β的三角函数表示)
如图,设∠AOC=α,∠BOC=β,P为射线OC上一点,PD⊥OA于D,PE⊥OB于E,则$\frac{PD}{PE}$等于$\frac{sinα}{sinβ}$ (用α、β的三角函数表示)
分析 根据已知条件得到∠PDO=∠PEO=90°,由三角函数的定义得到sinα=$\frac{PD}{PO}$,sinβ=$\frac{PE}{PO}$,即可得到结论.
解答 解:∵PD⊥OA于D,PE⊥OB于E,
∴∠PDO=∠PEO=90°,
∴sinα=$\frac{PD}{PO}$,sinβ=$\frac{PE}{PO}$,
∴$\frac{PD}{PE}$=$\frac{sinα}{sinβ}$.
故答案为:$\frac{sinα}{sinβ}$.
点评 此题考查了解直角三角形,理解直角三角形中边角之间的关系是解题的关键.

练习册系列答案
相关题目
11.下列各式中运算正确的是( )
| A. | 6a-5a=1 | B. | 3a2b-4ba2=-a2b | C. | 3a2+2a3=5a5 | D. | a2+a2=a4 |
6.在下列有理数中-5,0,|-3|,-|-2|,-(-1)中负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.抛物线$y=-{(x-\frac{1}{2})^2}$+3的对称轴是( )
| A. | 直线$x=-\frac{1}{2}$ | B. | 直线$x=\frac{1}{2}$ | C. | 直线x=3 | D. | 直线x=-3 |
