题目内容
2.在△ABC中,∠A,∠B为锐角,sinA=$\frac{1}{2}$,tanB=$\frac{\sqrt{3}}{3}$.则△ABC的形状为等腰三角形.分析 根据特殊角的三角函数值求出∠A和∠B的度数,然后判断形状.
解答 解:在△ABC中,
∵∠A,∠B为锐角,sinA=$\frac{1}{2}$,tanB=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,∠B=30°,
则∠C=120°,
故△ABC为等腰三角形.
故答案为:等腰三角形.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
11.抛物线$y=-{(x-\frac{1}{2})^2}$+3的对称轴是( )
| A. | 直线$x=-\frac{1}{2}$ | B. | 直线$x=\frac{1}{2}$ | C. | 直线x=3 | D. | 直线x=-3 |

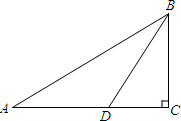 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=$\frac{\sqrt{3}}{3}$,AD=20.求BC的长.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,tan A=$\frac{\sqrt{3}}{3}$,AD=20.求BC的长.