题目内容
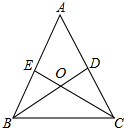 已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.(1)判断点O是否在∠BAC的角平分线上,并说明理由;
(2)求证:△ABC是等腰三角形;
(3)连接DE,那么DE与BC是否平行?为什么?
考点:全等三角形的判定与性质,等腰三角形的判定
专题:
分析:(1)由BD,CE是两条高就可以得出∠BEC=∠CDB=90°,由OB=OC就可以得出∠BCE=∠DBC,就可以得出△BCE≌△CBD,就可以得出CE=BD,得出OE=OD,得出结论;
(2)由△BCE≌△CBD就可以得出∠EBD=∠DCB,得出AB=AC,从而得出结论;
(3)由△BCE≌△CBD可以得出CD=BE,就可以得出AD=AE,得出∠AED=
(180°-∠A),由∠ABC=
(180°-∠A),得出∠AED=∠ABC而得出结论.
(2)由△BCE≌△CBD就可以得出∠EBD=∠DCB,得出AB=AC,从而得出结论;
(3)由△BCE≌△CBD可以得出CD=BE,就可以得出AD=AE,得出∠AED=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)点O在∠BAC的角平分线上.
理由:∵BD,CE是△ABC的两条高,
∴∠BEC=∠CDB=90°.
∵OB=OC,
∴∠BCE=∠DBC.
在△BCE和△CBD中,
,
∴△BCE≌△CBD(AAS),
∴CE=BD,
∴CE-OC=BD-OB,
∴OE=OD.
∴点O是否在∠BAC的角平分线上;
(2)∵△BCE≌△CBD,
∴∠EBD=∠DCB.
∴AB=AC,
∴△ABC是等腰三角形;
(3)DE∥BC.
理由:如图1,
∵△BCE≌△CBD,
∴BE=CD,
∴AB-BE=AC-CD,
∴AE=AD,
∴∠AED=∠ADE,
∴∠AED=
(180°-∠A).
∵∠EBD=∠DCB,
∴∠ABC=
(180°-∠A),
∴∠AED=∠ABC,
∴DE∥BC.
理由:∵BD,CE是△ABC的两条高,
∴∠BEC=∠CDB=90°.
∵OB=OC,
∴∠BCE=∠DBC.

在△BCE和△CBD中,
|
∴△BCE≌△CBD(AAS),
∴CE=BD,
∴CE-OC=BD-OB,
∴OE=OD.
∴点O是否在∠BAC的角平分线上;
(2)∵△BCE≌△CBD,
∴∠EBD=∠DCB.
∴AB=AC,
∴△ABC是等腰三角形;
(3)DE∥BC.
理由:如图1,
∵△BCE≌△CBD,
∴BE=CD,
∴AB-BE=AC-CD,
∴AE=AD,
∴∠AED=∠ADE,
∴∠AED=
| 1 |
| 2 |
∵∠EBD=∠DCB,
∴∠ABC=
| 1 |
| 2 |
∴∠AED=∠ABC,
∴DE∥BC.
点评:本题考查了等腰三角形的判定及性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,已知一次函数y=ax-2的图象与反比例函数y=
如图,已知一次函数y=ax-2的图象与反比例函数y= 作图题:(不要求写作法)
作图题:(不要求写作法)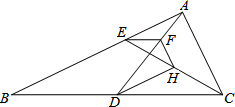 如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,连接AD,E为AB上一点,过E作EF∥BC交AD于F.
如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,连接AD,E为AB上一点,过E作EF∥BC交AD于F.