题目内容
已知
+4m2+1=4m,求
+
的值.
| m+n |
| m-n |
| m |
考点:配方法的应用,非负数的性质:偶次方,非负数的性质:算术平方根
专题:
分析:利用配方法对已知等式进行变形,得到:
+4(m-
)2=0,由非负数的性质得到m、n的值,然后将其代入所求的代数式进行求值即可.
| m+n |
| 1 |
| 2 |
解答:解:由
+4m2+1=4m,得
+4(m-
)2=0,
则
,
解得
.
所以
+
=
+
=1+
.
| m+n |
| m+n |
| 1 |
| 2 |
则
|
解得
|
所以
| m-n |
| m |
|
|
| ||
| 2 |
点评:此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
已知函数y=3x2-6x+k(k为常数)的图象经过点A(0.8,y1),B(1.1,y2),C(
,y3),则有( )
| 2 |
| A、y1<y2<y3 |
| B、y1>y2>y3 |
| C、y3>y1>y2 |
| D、y1>y3>y2 |
 如图,已知AB=DE,AC=DF,EC=BF,证明:AE=DB.
如图,已知AB=DE,AC=DF,EC=BF,证明:AE=DB.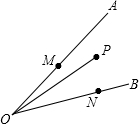 如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是
如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是