题目内容
已知函数y=3x2-6x+k(k为常数)的图象经过点A(0.8,y1),B(1.1,y2),C(
,y3),则有( )
| 2 |
| A、y1<y2<y3 |
| B、y1>y2>y3 |
| C、y3>y1>y2 |
| D、y1>y3>y2 |
考点:二次函数图象上点的坐标特征
专题:
分析:根据函数解析式的特点,其对称轴为x=1,图象开口向上,由于A(0.8,y1)在对称轴的左侧,根据二次函数图象的对称性可知,对称点为(1.2,y1),在y轴的右边y随x的增大而增大,可判断y2<y1<y3.
解答:解:∵函数y=3x2-6x+k(k为常数),
∴对称轴为x=1,图象开口向上;
∴A(0.8,y1)在对称轴的左侧,根据二次函数图象的对称性可知,对称点为(1.2,y1),在y轴的右边y随x的增大而增大,
因为1.1<1.2<
,于是y2<y1<y3
故选:C.
∴对称轴为x=1,图象开口向上;
∴A(0.8,y1)在对称轴的左侧,根据二次函数图象的对称性可知,对称点为(1.2,y1),在y轴的右边y随x的增大而增大,
因为1.1<1.2<
| 2 |
故选:C.
点评:本题考查了函数图象上的点的坐标与函数解析式的关系,同时考查了函数的对称性及增减性.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
等腰三角形的一个角是80°,则它的底角度数为( )
| A、50° | B、80° |
| C、80°或50° | D、不确定 |
下面两个数互为相反数的是( )
A、
| ||
B、
| ||
C、-2.75和2
| ||
| D、9和-(-9) |
 如图所示,在形状为平行四边形的一块地中,有一条小路EFG,现在想把它改为过点G的直路,要求小路两侧土地面积都不变,请在图中画出改动后的小路.
如图所示,在形状为平行四边形的一块地中,有一条小路EFG,现在想把它改为过点G的直路,要求小路两侧土地面积都不变,请在图中画出改动后的小路.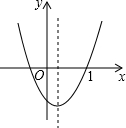 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则c、△(△=b2-4ac)与零的大小关系是c
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则c、△(△=b2-4ac)与零的大小关系是c 如图,A、B是双曲线y=
如图,A、B是双曲线y=