题目内容
先化简,再求值:
,其中x=2+
,y=2-
.
| x |
| x+2y |
|
| 3 |
| 3 |
考点:二次根式的化简求值
专题:计算题
分析:先把二次根式化简得到原式=
•
•(x+2y),然后约分得到原式=
,然后计算xy的值,再利用整体代入的方法计算.
| x |
| x+2y |
| ||
| x |
| xy |
解答:解:原式=
•
=
•
•(x+2y)
=
,
∵x=2+
,y=2-
,
∴xy=4-3=1,
∴原式=
=1.
| x |
| x+2y |
|
=
| x |
| x+2y |
| ||
| x |
=
| xy |
∵x=2+
| 3 |
| 3 |
∴xy=4-3=1,
∴原式=
| 1 |
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
 如图,下列式子正确的是( )
如图,下列式子正确的是( )| A、a+b>0 |
| B、a-c>0 |
| C、c-a>0 |
| D、a-b<0 |
下列说法正确的是( )
| A、有理数可分为正数,负数 |
| B、正数没有最大的数,有最小的数 |
| C、零既不是正数也不是负数 |
| D、带“+号”和带“-”号的数互为相反数 |
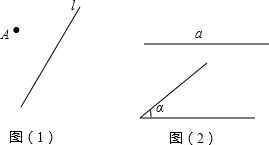 尺规作图:
尺规作图: