题目内容
如图，已知⊙O的半径为10，点C、D是直径AB同侧圆周上的两点， |
| AC |
|
| BD |
考点：轴对称-最短路线问题
专题：
分析：根据轴对称，作出点C关于AB的对称点E，连接DE交AB于点P，此时PC+PD最小，就等于DE的长．由题意可知∠DOE=120°，然后在△DOE中求出DE的长．
解答：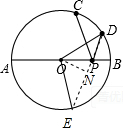
解：如图：点E是点C关于AB的对称点，根据对称性可知：PC=PE．
由两点之间线段最短，此时DE的长就是PC+PD的最小值．
∵
的度数为96°，
的度数为36°，
∴
的度数为96，
的度数为84°，∴
的度数=84°+36°=120°．
∴∠DOE=120°，∠E=30°，
过O作ON⊥DE于N，则DE=2DN，
∵cos30°=
，
∴EN=
OE=
×10=5
，
即DE=2EN=10
，
所以PC+PD的最小值为10
．
故答案为10
．
解：如图：点E是点C关于AB的对称点，根据对称性可知：PC=PE．由两点之间线段最短，此时DE的长就是PC+PD的最小值．
∵
|
| AC |
|
| BD |
∴
|
| AE |
|
| BE |
|
| DBE |
∴∠DOE=120°，∠E=30°，
过O作ON⊥DE于N，则DE=2DN，
∵cos30°=
| EN |
| OE |
∴EN=
| ||
| 2 |
| ||
| 2 |
| 3 |
即DE=2EN=10
| 3 |
所以PC+PD的最小值为10
| 3 |
故答案为10
| 3 |
点评：本题考查了垂径定理以及轴对称的性质，根据轴对称找出点C的对称点E，由两点之间线段最短，确定DE的长就是PC+PD的最小值是本题的关键．
练习册系列答案
相关题目
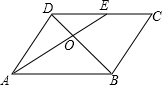如图，在?ABCD中，E为CD中点，AE与BD相交于点O，若S△DOE=2cm2，则S△AOB等于（ ）cm2．
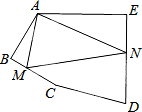如图，在五边形ABCDE中，∠BAE=125°，∠B=∠E=90°，AB=BC，AE=DE，在BC、DE上分别找一点M、N，使得△AMN周长最小时，∠AMN+∠ANM的度数为