题目内容
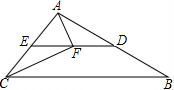 如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE=
如图,在△ABC中,∠ACB=58°,D,E分别是AB,AC中点.点F在线段DE上,且AF⊥CF,则∠FAE=考点:三角形中位线定理,直角三角形斜边上的中线
专题:
分析:由点D,E分别是AB,AC的中点可EF是三角形ABC的中位线,所以EF∥BC,再有平行线的性质和在直角三角形中,斜边上的中线等于斜边的一半的性质可证明三角形EFC是等腰三角形,利用等腰三角形的性质可求出∠ECF的度数,进而求出∠FAE的度数.
解答:解:∵D,E分别是AB,AC的中点,
∴EF是三角形ABC的中位线,
∴EF∥BC,
∴∠EFC=∠ECF,
∵AF⊥CF,
∴∠AFC=90°,
∵E分AC的中点,
∴EF=
AC,AE=CE,
∴EF=CE,
∴∠EFC=∠ECF,
∴∠ECF=∠EFC=
∠ACB=29°,
∴∠FAE的度数为90°-29°=61°,
故答案为:61.
∴EF是三角形ABC的中位线,
∴EF∥BC,
∴∠EFC=∠ECF,
∵AF⊥CF,
∴∠AFC=90°,
∵E分AC的中点,
∴EF=
| 1 |
| 2 |
∴EF=CE,
∴∠EFC=∠ECF,
∴∠ECF=∠EFC=
| 1 |
| 2 |
∴∠FAE的度数为90°-29°=61°,
故答案为:61.
点评:本题考查了三角形的中位线的性质、直角三角形的性质、等腰三角形的判定和性质、平行线的性质以及三角形的内角和定理的运用,题目的难度不大.

练习册系列答案
相关题目
若点A(a,b)在第四象限,则点(b-a,a-b)在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
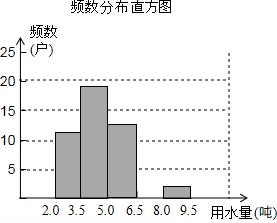 某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理:
某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理: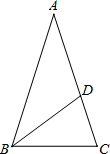 如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x. 图中直线是由直线l向上平移1个单位,向左平移2个单位得到的,则直线l对应的一次函数关系式为
图中直线是由直线l向上平移1个单位,向左平移2个单位得到的,则直线l对应的一次函数关系式为 如图,矩形ABCD中,AD=
如图,矩形ABCD中,AD= 如图,在梯形ABCD中,AD∥BC,BD=CD,AD=1,BC=8,∠BDC=90°,则AB的长为
如图,在梯形ABCD中,AD∥BC,BD=CD,AD=1,BC=8,∠BDC=90°,则AB的长为