题目内容
11.先化简,再求值:$\frac{1}{x+1}$-$\frac{x+2}{x-1}$•$\frac{{x}^{2}-2x+1}{{x}^{2}+4x+4}$,再选择一个理想的x的值代入求值.分析 原式第二项约分后,两项通分并利用同分母分式的减法法则计算,得到最简结果,把x=0代入计算即可求出值.
解答 解:原式=$\frac{1}{x+1}$-$\frac{x+2}{x-1}$•$\frac{(x-1)^{2}}{(x+2)^{2}}$=$\frac{1}{x+1}$-$\frac{x-1}{x+2}$=$\frac{x+2-{x}^{2}+1}{{x}^{2}+3x+2}$=$\frac{-{x}^{2}+x+3}{{x}^{2}+3x+2}$,
当x=0时,原式=$\frac{3}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列语句:①不循环小数是无理数;②两个无理数的和还是无理数;③有理数与无理数的和是无理数;④两个无理数之积一定还是无理数;⑤无理数与有理数之积可能是有理数.其中错误的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.某大学生利用暑假参与一家旅行社的经营,了解到一条成本为500元/人的旅游线路的游客人数y(人/月)与旅游报价x(元/人)之间的关系如表:(旅游主管部门规定该旅游吸路线报价在800元/人~1500元/人之间)
(1)要将该旅游线路每月游客人数控制在200人以内(含200人),求该旅游线路报价的取值范围;
(2)求这条旅游线路所获得的利润w(元)与旅游报价x(元/人)之间的函数关系式.
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
| 旅游报价x元/人 | 游客人数y(人/月) |
| 800≤x<1200 | -x+1300 |
| 1200≤x<1500 | 100 |
(2)求这条旅游线路所获得的利润w(元)与旅游报价x(元/人)之间的函数关系式.
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
 如图,过点P(0,-2)的直线l与抛物线y=x2只有一个公共点M,求点M的坐标.
如图,过点P(0,-2)的直线l与抛物线y=x2只有一个公共点M,求点M的坐标.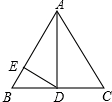 如图,在等边△ABC中,AD是中线,DE⊥AB,垂足为E,若BC=4cm.则DE的长$\sqrt{3}$cm.
如图,在等边△ABC中,AD是中线,DE⊥AB,垂足为E,若BC=4cm.则DE的长$\sqrt{3}$cm.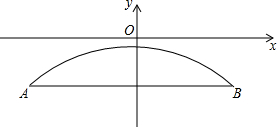 有一个抛物线形的拱形桥,若抛物线的解析式为y=-$\frac{1}{75}$x2-1.
有一个抛物线形的拱形桥,若抛物线的解析式为y=-$\frac{1}{75}$x2-1.