题目内容
3.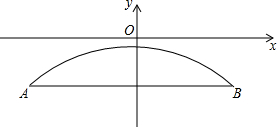 有一个抛物线形的拱形桥,若抛物线的解析式为y=-$\frac{1}{75}$x2-1.
有一个抛物线形的拱形桥,若抛物线的解析式为y=-$\frac{1}{75}$x2-1.(1)求拱顶离桥面的高度;
(2)若拱顶离水面的高度为27m,求桥的跨度.
分析 (1)当x=0时,y=-1,即可求出拱顶离桥面的高度;
(2)拱顶离水面的高度为27m,则y=-28,代入函数表达式求出x,即可求桥的跨度.
解答 解:(1)当x=0时,代入y=-$\frac{1}{75}$x2-1.
得:y=-1.
所以拱顶离桥面的高度为1米;
(2)由于拱顶离水面的高度为27m,则y=-28,
把y=-28,代入y=-$\frac{1}{75}$x2-1.
得:-28=-$\frac{1}{75}$x2-1.
解得:x=±45.
所以桥的跨度为90米.
点评 本题主要考查了二次函数的实际应用,正确理解实际问题的数学意义是解决问题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
11.如图1,四边形ABCD、AEFG都是正方形,连接DE、BG.
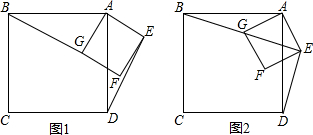
(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.

(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.
18.在直角坐标系中,线段AB与x轴平行,则A、B两点坐标的特点是( )
| A. | 横坐标相同 | B. | 纵坐标相同 | ||
| C. | 横纵坐标都相同 | D. | 横纵坐标都不相同 |
15.关于x的方程$\frac{2x+a}{x-1}$=1的解是负数,则a的取值范围是( )
| A. | a>-1 | B. | a>-1或a≠-2 | C. | a<-1 | D. | a<-1且a≠0 |
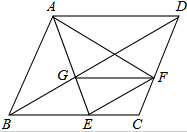 已知,如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
已知,如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.