题目内容
6.某大学生利用暑假参与一家旅行社的经营,了解到一条成本为500元/人的旅游线路的游客人数y(人/月)与旅游报价x(元/人)之间的关系如表:(旅游主管部门规定该旅游吸路线报价在800元/人~1500元/人之间)| 旅游报价x元/人 | 游客人数y(人/月) |
| 800≤x<1200 | -x+1300 |
| 1200≤x<1500 | 100 |
(2)求这条旅游线路所获得的利润w(元)与旅游报价x(元/人)之间的函数关系式.
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
分析 (1)根据题意得出-x+1300≤200,解不等式即可;
(2)利用利润=售价-成本,分别求出在800≤x<1200和1200≤x≤1500时,y与x的函数关系式;
(3)当800≤x<1200时,w=(x-500)(-x+1300)=-(x-900)2+360000,求出一个最大值w1,当1200≤x≤1500时,求出一个最大值w2,然后比较两者的大小.
解答 解:(1)由题意得-x+1300≤200,
解得x≥1100;
所以该旅游线路报价的取值范围1100≤x<1200;
(2)这条旅游线路所获得的利润w(元)与旅游报价x(元/人)之间的函数关系式:
w=$\left\{\begin{array}{l}{(x-500)(-x+1300)(800≤x<1200)}\\{100(x-500)(1200≤x<1500)}\end{array}\right.$;
(3)当800≤x≤1200时,w=(x-500)(-x+1300)=-x2+1800x+450000=-(x-900)2+360000,
∵-1<0,
∴当x=900时,w有最大值w1,且w1=360000,
当1200≤x<1500时,∵w=100(x-500)=100x-50000,
∵100>0
∴w随x的增大而增大,
当x=1500时,w最大,
于是,x=1500时,w有最大值w2,且w2=100×1500-50000=100000,
∵w1>w2,
∴当这条旅游线路的旅游报价为900元时,可获得最大利润;最大利润是360000元.
点评 本题主要考查二次函数的应用的知识点,解答本题的关键是熟练掌握二次函数的性质和一次函数的性质以及最值得求法,此题难度不大.

练习册系列答案
相关题目
11.如图1,四边形ABCD、AEFG都是正方形,连接DE、BG.
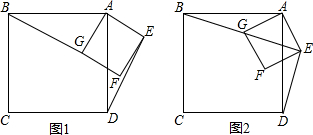
(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.

(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.
18.在直角坐标系中,线段AB与x轴平行,则A、B两点坐标的特点是( )
| A. | 横坐标相同 | B. | 纵坐标相同 | ||
| C. | 横纵坐标都相同 | D. | 横纵坐标都不相同 |
15.关于x的方程$\frac{2x+a}{x-1}$=1的解是负数,则a的取值范围是( )
| A. | a>-1 | B. | a>-1或a≠-2 | C. | a<-1 | D. | a<-1且a≠0 |
 如图,在正方形ABCD中,E为BC的中点,F是CD的中点.求$\frac{AF}{EF}$的值.
如图,在正方形ABCD中,E为BC的中点,F是CD的中点.求$\frac{AF}{EF}$的值. 某市火车站开设了普通售票窗口和自动打印车票的无人售票窗口,某日从早上8时到上午11时,每个普通售票窗口售出车票数y1(张),每个无人售票窗口售出车票y2(张),如图所示,则上午11点,普通售票窗口开放5个,两种窗口共售出的车票数不少于2100张,无人售票窗口至少开放5个.
某市火车站开设了普通售票窗口和自动打印车票的无人售票窗口,某日从早上8时到上午11时,每个普通售票窗口售出车票数y1(张),每个无人售票窗口售出车票y2(张),如图所示,则上午11点,普通售票窗口开放5个,两种窗口共售出的车票数不少于2100张,无人售票窗口至少开放5个.