题目内容
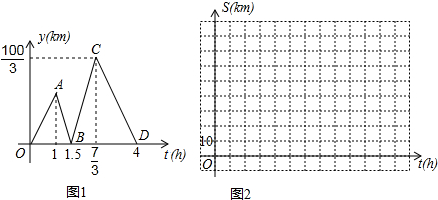
7.方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过$\frac{4}{3}$h与乙相遇,问丙出发后多少时间与甲相遇?
分析 (1)利用待定系数法求函数解析式,即可解答;
(2)先求出甲、乙的速度、所以OA的函数解析式为:y=20t(0≤t≤1),所以点A的纵坐标为20,根据当20<y<30时,得到20<40t-60<30,或20<-20t+80<30,解不等式组即可;
(3)得到S甲=60t-60($1≤t≤\frac{7}{3}$),S乙=20t(0≤t≤4),画出函数图象即可;
(4)确定丙距M地的路程S丙与时间t的函数表达式为:S丙=-40t+80(0≤t≤2),根据S丙=-40t+80与S甲=60t-60的图象交点的横坐标为$\frac{7}{5}$,所以丙出发$\frac{5}{7}$h与甲相遇.
解答 解:(1)直线BC的函数解析式为y=kt+b,
把(1.5,0),($\frac{7}{3},\frac{100}{3}$)代入得:$\left\{\begin{array}{l}{1.5k+b=0}\\{\frac{7}{3}k+b=\frac{100}{3}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=40}\\{b=-60}\end{array}\right.$,
∴直线BC的解析式为:y=40t-60;
设直线CD的函数解析式为y1=k1t+b1,
把($\frac{7}{3},\frac{100}{3}$),(4,0)代入得:$\left\{\begin{array}{l}{\frac{7}{3}{k}_{1}+{b}_{1}=\frac{100}{3}}\\{4{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-20}\\{{b}_{1}=80}\end{array}\right.$,
∴直线CD的函数解析式为:y=-20t+80.
(2)设甲的速度为akm/h,乙的速度为bkm/h,根据题意得;
$\left\{\begin{array}{l}{0.5a=1.5b}\\{a(\frac{7}{3}-1)=\frac{7}{3}b+\frac{100}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=60}\\{b=20}\end{array}\right.$,
∴甲的速度为60km/h,乙的速度为20km/h,
∴OA的函数解析式为:y=20t(0≤t≤1),所以点A的纵坐标为20,
当20<y<30时,
即20<40t-60<30,或20<-20t+80<30,
解得:$2<t<\frac{9}{4}$或$\frac{5}{2}<t<3$.
(3)根据题意得:S甲=60t-60($1≤t≤\frac{7}{3}$)
S乙=20t(0≤t≤4),
所画图象如图2所示:
(4)当t=$\frac{4}{3}$时,${S}_{乙}=\frac{80}{3}$,丙距M地的路程S丙与时间t的函数表达式为:
S丙=-40t+80(0≤t≤2),
如图3,
S丙=-40t+80与S甲=60t-60的图象交点的横坐标为$\frac{7}{5}$,
所以丙出发$\frac{7}{5}$h与甲相遇.
点评 本题考查了一次函数的应用,解决本题的关键是根据图象获取相关信息,利用待定系数法求函数解析式.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案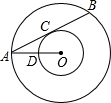 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
 如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
| A. | -$\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
| A. | a5 | B. | -a5 | C. | a6 | D. | -a6 |
 小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高?
小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高?