题目内容
12. 如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )| A. | 100° | B. | 108° | C. | 110° | D. | 120° |
分析 利用邻补角的定义,先求出∠ADE的外角,再利用多边形的内角和公式求∠AED的度数即可.
解答 解:根据五边形的内角和公式可知,五边形ABCDE的内角和为(5-2)×180°=540°,
根据邻补角的定义可得∠EAB=∠ABC=∠BCD=∠CDE=180°-70°=110°,
所以∠AED=540°-110°×4=100°.
故选A.
点评 本题考查了多边形的内角和公式和邻补角的定义.多边形的内角和为:180°(n-2).

练习册系列答案
相关题目
3.若x=-1是关于x的一元二次方程ax2+bx-2=0(a≠0)的一个根,则2015-2a+2b的值等于( )
| A. | 2015 | B. | 2011 | C. | 2018 | D. | 2013 |
20.若a2=25,|b|=3,则a+b=( )
| A. | 8 | B. | ±8 | C. | ±2 | D. | ±8或±2 |
7.在下列各数中,最大的数是( )
| A. | -3 | B. | 0 | C. | 2 | D. | $\sqrt{3}$ |
4. 如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
 如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )| A. | 40° | B. | 50° | ||
| C. | 80° | D. | 随点B、C的移动而变化 |
2.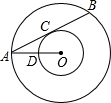 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
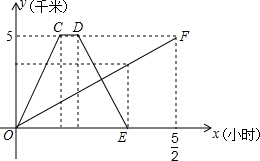 A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题:
A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题: