题目内容
14.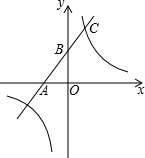 如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
分析 (1)根据OA=OB和点B的坐标易得点A坐标,再将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,;
(2)由B是线段AC的中点,可得C点坐标,将C点坐标代入y=$\frac{k}{x}$(k≠0)可确定反比例函数的解析式.
解答 解:(1)∵OA=OB,点B的坐标为(0,2),
∴点A(-2,0),
点A、B在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}{-2k+b=0}\\{b=2}\end{array}\right.$,
解得k=1,b=2,
∴一次函数的解析式为y=x+2.
(2)∵B是线段AC的中点,
∴点C的坐标为(2,4),
又∵点C在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=8;
∴反比例函数的解析式为y=$\frac{8}{x}$.
点评 本题考查了用待定系数法求函数解析式,过某个点,这个点的坐标应适合这个函数解析式.

练习册系列答案
相关题目
4. 如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
 如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )
如图,∠MAN=100°,点B、C是射线AM、AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小( )| A. | 40° | B. | 50° | ||
| C. | 80° | D. | 随点B、C的移动而变化 |
2.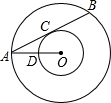 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
19.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
3. 如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )
如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )
 如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )
如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
4.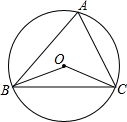 如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
 如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )| A. | 22° | B. | 26° | C. | 32° | D. | 68° |
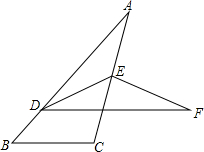 如图,在△ABC中,点D、E分别是AB、AC上的点,将△ABC沿DE折叠,点A落到F的位置,已知DF∥BC,∠B=50°,∠CEF=80°,说明:EA=ED.
如图,在△ABC中,点D、E分别是AB、AC上的点,将△ABC沿DE折叠,点A落到F的位置,已知DF∥BC,∠B=50°,∠CEF=80°,说明:EA=ED.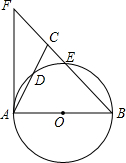 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.