题目内容
11.小明到服装店进行社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元,乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.(1)若购进这100件服装的费用不得超过7500元,则甲种服装最多购进多少件??
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
分析 (1)设甲种服装购进x件,则乙种服装购进(100-x)件,然后根据购进这100件服装的费用不得超过7500元,列出不等式解答即可;
(2)首先求出总利润W的表达式,然后针对a的不同取值范围进行讨论,分别确定其进货方案.
解答 解:(1)设甲种服装购进x件,则乙种服装购进(100-x)件,
根据题意得:
$\left\{\begin{array}{l}{x≥65}\\{80x+60(100-x)≤7500}\end{array}\right.$,
解得:65≤x≤75,
∴甲种服装最多购进75件;
(2)设总利润为W元,
W=(120-80-a)x+(90-60)(100-x)
即w=(10-a)x+3000.
①当0<a<10时,10-a>0,W随x增大而增大,
∴当x=75时,W有最大值,即此时购进甲种服装75件,乙种服装25件;
②当a=10时,所以按哪种方案进货都可以;
③当10<a<20时,10-a<0,W随x增大而减小.
当x=65时,W有最大值,即此时购进甲种服装65件,乙种服装35件.
点评 本题考查了一元一次方程的应用,不等式组的应用,以及一次函数的性质,正确利用x表示出利润是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.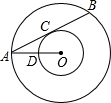 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=$\frac{1}{2}$,则AB的长是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
19.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
16.计算(-a3)2的结果是( )
| A. | a5 | B. | -a5 | C. | a6 | D. | -a6 |
3. 如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )
如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )
 如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )
如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
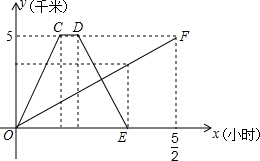 A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题:
A、B两地之间有一条笔直的公路,甲乙两人从A地前往B地,甲骑自行车,乙步行,甲到达B地并在B地停留十分钟后,再按原路原速返回,当甲返回到A地时,乙距B地1.5千米,他们各自距A地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象信息解答下列问题: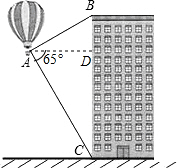 如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)