题目内容
11.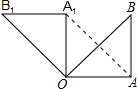 如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.(1)线段OA1的长是5,∠AOB1的度数是135°;
(2)连接AA1,求证:四边形OAA1B1是平行四边形.
分析 (1)△OAB是等腰直角三角形,△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,则△OAB≌△OA1B1,根据全等三角形的性质即可求解.
(2)可证明OA∥A1B1且相等,即可证明四边形OAA1B1是平行四边形.
解答 (1)解:∵△OAB≌△OA1B1,
∴OA1=OA=5;
∵△OAB是等腰直角三角形,
∴∠A1OB=45°
∴∠AOB1=∠BOB1+∠BOA=90+45=135°.
故答案为5,135°;
(2)证明:∵∠AOA1=∠OA1B1=90°,
∴OA∥A1B1,
又∵OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.
点评 此题主要考查了旋转的性质和平行四边形的判定,解题的关键是得出OA∥A1B1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.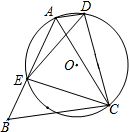 已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
 已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
6.如图,A,B,C,D为圆O的四等分点,动点P从圆心O出发,沿O-C-D-O-C-D-O路线作匀速运动,设运动时间为x(秒),∠APB的度数为y(度),右图函数图象表示y与x之间函数关系,则点M的横坐标应为( )


| A. | 2 | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$+1 | D. | $\frac{π}{2}$+3 |
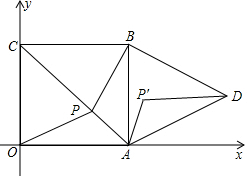 如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.
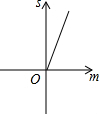
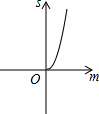
如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.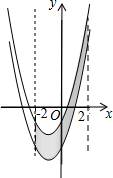 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )

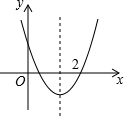 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列有4个结论:①b2-4ac>0;②abc<0;③b<a+c;④4a+b=1.请你将正确结论的番号都写出来①②③.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列有4个结论:①b2-4ac>0;②abc<0;③b<a+c;④4a+b=1.请你将正确结论的番号都写出来①②③.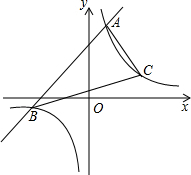 已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.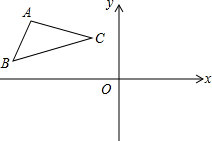 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.
如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.