题目内容
14.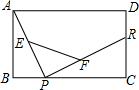 如图,已知矩形ABCD中,R是边CD的中点,P是边BC上一动点,E、F分别是AP、RP的中点,设BP的长为x,EF的长为y,当P在BC上从B向C移动时,y与x的大致图象是( )
如图,已知矩形ABCD中,R是边CD的中点,P是边BC上一动点,E、F分别是AP、RP的中点,设BP的长为x,EF的长为y,当P在BC上从B向C移动时,y与x的大致图象是( )| A. | 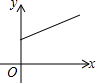 | B. | 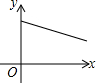 | C. | 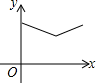 | D. |  |
分析 因为R不动,所以AR不变.根据中位线定理,EF不变.
解答 解:连接AR.
因为E、F分别是AP、RP的中点,
则EF为△APR的中位线,
所以EF=$\frac{1}{2}$AR,为定值.
所以线段EF的长不改变.
故选:D.
点评 本题考查了三角形的中位线定理,只要三角形的边AR不变,则对应的中位线的长度就不变.

练习册系列答案
相关题目
2.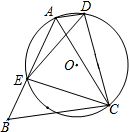 已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
 已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
6.如图,A,B,C,D为圆O的四等分点,动点P从圆心O出发,沿O-C-D-O-C-D-O路线作匀速运动,设运动时间为x(秒),∠APB的度数为y(度),右图函数图象表示y与x之间函数关系,则点M的横坐标应为( )


| A. | 2 | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$+1 | D. | $\frac{π}{2}$+3 |
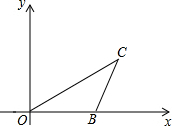 已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,
已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,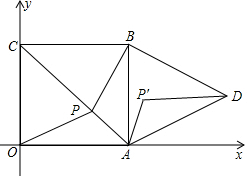 如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.
如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.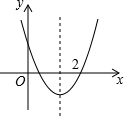 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列有4个结论:①b2-4ac>0;②abc<0;③b<a+c;④4a+b=1.请你将正确结论的番号都写出来①②③.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列有4个结论:①b2-4ac>0;②abc<0;③b<a+c;④4a+b=1.请你将正确结论的番号都写出来①②③.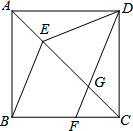 如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.