题目内容
20.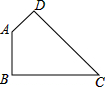 如图,在四边形ABCD中,∠BAD=135°,∠ABC=∠ADC=90°,DC=6,AD=2,求四边形ABCD的面积.
如图,在四边形ABCD中,∠BAD=135°,∠ABC=∠ADC=90°,DC=6,AD=2,求四边形ABCD的面积.
分析 如上图所示,延长AB,延长DC,相交于E点.△ADE是等腰直角三角形,AD=DE=2,则可以求出△ADE的面积;由∠BAD=135°,可得∠C=∠AED=45°,所以△CBE是等腰直角三角形,CE=6+2=8,可得BE=BC=4$\sqrt{2}$,则可以求出△CBE的面积;那么四边形ABCD的面积是两个三角形的面积之差.
解答 解:∵四边形ABCD中,∠BAD=135°,∠ABC=∠ADC=90°,
∴∠C=45°,
延长AB,延长DC,相交于E点,得到两个等腰直角三角形△ADE和△CBE,
由等腰直角三角形的性质得: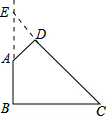
DE=AD=2,
易得,CE=6+2=8,
∴BE=BC=8×sin45°=8×$\frac{\sqrt{2}}{2}$=4$\sqrt{2}$,
那么四边形ABCD的面积是:
4$\sqrt{2}$×4$\sqrt{2}$÷2-2×2÷2
=16-2
=14,
答:四边形ABCD的面积是14.
点评 此题考查了等腰直角三角形的性质以及三角形的面积公式的运用,解题的关键是作延长线,找到交点,组成新图形,是解决此题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
10. 如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
 如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )| A. | 50° | B. | 59° | C. | 60° | D. | 62° |
 如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.
如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.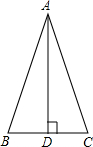 如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.
如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.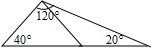 如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形.
如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形.