题目内容
11.某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现采用尽量提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销售量就减少10件.问:①应将售价提为多少元时,才能使所赚利润为700元?
②当售价提高多少元时,所获利润最大?并求出最大利润.
分析 (1)根据等量关系“利润=(售价-进价)×销量”列出函数关系式.
(2)根据(1)中的函数关系式求得利润最大值.
解答 解:(1)设每件售价提高x元时,才能使每天利润为700元,
(10-8+x)(200-20x)=700,
解得:x1=3(舍去),x2=5.
∴应将每件售价定为15元.
(2)设利润为y:
则y=(2+x)(200-2x)=-20(x-4)2+720,
∴当售价提高4元时,获利最大,最大利润720元.
点评 此题主要考查了二次函数的应用以及一元二次方程的应用,根据二次函数的性质求实际问题的最值是中考中考查重点,应重点掌握.

练习册系列答案
相关题目
1.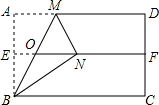 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )
如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )
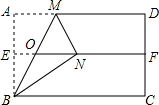 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )
如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
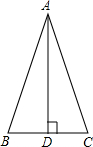 如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.
如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.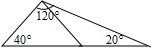 如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形.
如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形. 如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是$\frac{2}{3}\sqrt{3}$.
如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是$\frac{2}{3}\sqrt{3}$.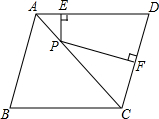 如图,在菱形ABCD中,点P是对角线AC上一点,PE⊥AD于点E,PF⊥CD于点F,若AB=5,菱形ABCD的面积为24,求PE+PF的值.
如图,在菱形ABCD中,点P是对角线AC上一点,PE⊥AD于点E,PF⊥CD于点F,若AB=5,菱形ABCD的面积为24,求PE+PF的值.