题目内容
2.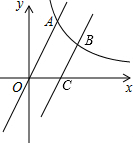 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.(1)求k的值;
(2)点B为此反比例函数图象上一点,其纵坐标为3.过点B作CB∥OA,交x轴于点C,直接写出线段OC的长.
分析 (1)首先求出点A的坐标为(2,6),把点A(2,6)代入y=$\frac{k}{x}$即可求出k的值;
(2)求出点B的坐标为B(4,3),设直线BC的解析式为y=3x+b,把点B(4,3)代入求出b=-9,得出直线BC的解析式为y=3x-9,求出当y=0时,x=3即可.
解答 解:(1)∵点A在直线y=3x上,其横坐标为2.
∴y=3×2=6,
∴A(2,6),
把点A(2,6)代入y=$\frac{k}{x}$得:6=$\frac{k}{2}$,
解得:k=12,
(2)由(1)得:y=$\frac{12}{x}$,
∵点B为此反比例函数图象上一点,其纵坐标为3,
∴x=$\frac{12}{3}$=4,
∴B(4,3),
∵CB∥OA,
∴设直线BC的解析式为y=3x+b,
把点B(4,3)代入得:3×4+倍,解得:b=-9,
∴直线BC的解析式为y=3x-9,
当y=0时,3x-9=0,
解得:x=3,
∴C(3,0),
∴OC=3.
点评 本题考查了反比例函数图象与一次函数图象的交点、反比例函数解析式和一次函数解析式的求法;求出反比例函数解析式是解决问题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
13.设A、B都是关于x的5次多项式,则下列说法正确的是( )
| A. | A+B是关于x的5次多项式 | B. | A-B是关于x的4次多项式 | ||
| C. | AB是关于x的10次多项式 | D. | $\frac{A}{B}$是与x无关的常数 |
17.下列计算结果为x5的是( )
| A. | x3+x2 | B. | x6÷x | C. | (x2)3 | D. | x7-x2 |
 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是60°.
如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是60°.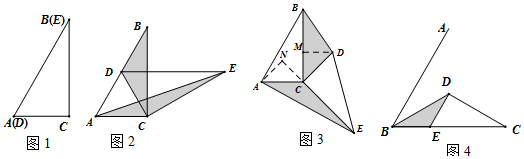
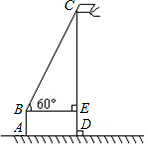 小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)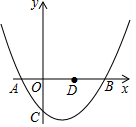 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.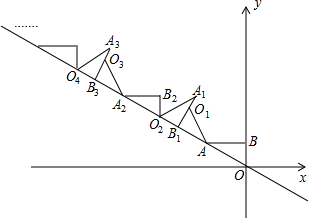 如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.
如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.