题目内容
15. 如图,在△ABC中,AB=AC=7,BC=5,AF⊥BC于F,BE⊥AC于E,D是AB的中点,则△DEF的周长是$\frac{19}{2}$.
如图,在△ABC中,AB=AC=7,BC=5,AF⊥BC于F,BE⊥AC于E,D是AB的中点,则△DEF的周长是$\frac{19}{2}$.
分析 根据直角三角形斜边上的中线等于斜边的一半可得DE=DF=$\frac{1}{2}$AB,EF=$\frac{1}{2}$BC,然后代入数据计算即可得解.
解答 解:∵AB=AC=7,BC=5,AF⊥BC于F,BE⊥AC于E,D是AB的中点,
∴△BCE是直角三角形,EF是Rt△BCE的中线,
EF=BF=FC=$\frac{1}{2}$BC=$\frac{5}{2}$,
又∵点D是AB的中点,
∴DF是Rt△AFB的中线,也是Rt△AEB的中线,
∴DE=DF=$\frac{1}{2}$AC=$\frac{7}{2}$,
∴三角形DEF的周长=DE+DF+EF=$\frac{7}{2}$+$\frac{7}{2}$+$\frac{5}{2}$=$\frac{19}{2}$,
故答案为$\frac{19}{2}$.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记各性质是解题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 实数a、b在数轴上的位置如图所示,请化简:|a-b|-$\sqrt{a^2}$-$\sqrt{{{(b+a)}^2}}$.
实数a、b在数轴上的位置如图所示,请化简:|a-b|-$\sqrt{a^2}$-$\sqrt{{{(b+a)}^2}}$.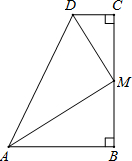 如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论:
如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论: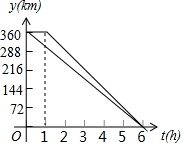 在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲、乙两车分别从A、B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.当甲车出发3.5小时时,两车相距330km.
在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲、乙两车分别从A、B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.当甲车出发3.5小时时,两车相距330km.