题目内容
16．某公园中央地上有一个大理石球，小明想测量球的半径，于是找了两块厚20cm的砖塞在球的两侧（如图所示），他量了下两砖之间的距离刚好是80cm，聪明的你，请你算出大石头的半径是（ ）
| A． | 40cm | B． | 30cm | C． | 20cm | D． | 50cm |
分析 如图，作辅助线；首先根据题意求出线段AD、DC的长度；设圆的半径为λ，运用勾股定理列出关于λ的方程，求出λ，即可解决问题．
解答 
解：如图，连接AB、OC交AB于点D；
则AB=80，CD=20，OD⊥AB；
设⊙O的半径为λ，则OD=λ-20；
在直角△AOD中，AD=40，
由勾股定理得：λ2=（λ-20）2+402
解得：λ=50．
故选D．
点评 该题主要考查了垂径定理、勾股定理及其应用问题；解题的方法是作辅助线，构造直角三角形；解题的关键是灵活运用垂径定理、勾股定理来分析、判断、解答．
练习册系列答案
相关题目
7．在Rt△ABC中，∠C=90°，AC：BC=1：2，则sinB的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{2\sqrt{5}}{5}$ |
4．
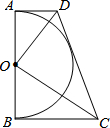如图，在直角梯形ABCD中AD∥BC．∠ABC=90°DC与以AB为直径的半圆⊙O相切，⊙O的半径为r，在下列结论：①OD⊥OC；②AD+BC=DC； ③S△AOD+S△BOC=S△DOC； ④AD•BC=r2中正确的个数有（ ）
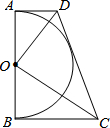如图，在直角梯形ABCD中AD∥BC．∠ABC=90°DC与以AB为直径的半圆⊙O相切，⊙O的半径为r，在下列结论：①OD⊥OC；②AD+BC=DC； ③S△AOD+S△BOC=S△DOC； ④AD•BC=r2中正确的个数有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
如图，CD⊥AB于点D，FE⊥AB于点E，∠1=∠2，试判断∠AGD与∠ACB的关系，并说明理由．
1．
如图，PA、PB是⊙O的切线，AC是⊙O的直径，∠P=62°，则∠BOC的度数为（ ）
如图，PA、PB是⊙O的切线，AC是⊙O的直径，∠P=62°，则∠BOC的度数为（ ）| A． | 60° | B． | 62° | C． | 31° | D． | 70° |
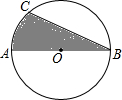如图，⊙O的半径为6cm，AB是⊙O的直径，BC是弦，∠ABC=30°，则图中阴影部分的面积为6π+9$\sqrt{3}$cm2（结果用无理数表示）
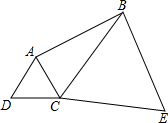如图，△ADC和△BCE都是等边三角形，已知BD2=AB2+BC2，那么∠ABC=30°．