题目内容
10.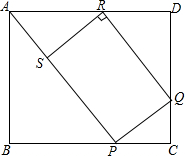 如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S.
如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S.(1)试说明四边形PQRS是矩形.
(2)设矩形PQRS的面积为y,求y与x的函数关系式;
(3)当四边形PQRS是正方形时,求CP的长.
分析 (1)根据等腰直角三角形的性质,可得∠QPC的度数,根据角的和差,可得∠SPQ的度数,根据平行线的判定,可得PQ与SR的关系,根据矩形的判定,可得答案;
(2)根据面积的和差,可得函数关系式;
(3)根据正方形的对角线垂直、相等且互相平分,可得PC与QC与QD的关系.
解答 (1)证明:∵矩形ABCD中,∠B=∠C=90°.
∵∠BAP=45°,
∴∠BPA=45°.
∵CP=CQ,
∴∠QPC=45°,
∴∠QPS=180°-45°-45°=90°,
∵RS⊥AP于点S,
∴∠RSA=90°=∠QPS,
∴SR∥PQ,
又∵PQ∥AP,
∴四边形PQRS是矩形;
(2)由面积的和差,得
y=x-$\frac{1}{2}$-$\frac{1}{2}$(x-1)2-$\frac{1}{2}$(2-x)2-$\frac{1}{2}$(2x-2)2,
化简,得y=-$\frac{3}{2}$x2+8x-$\frac{9}{2}$;
(3)由四边形PQRS是正方形,得
PR=SQ,PR⊥SQ,$\frac{1}{2}$PR=$\frac{1}{2}$SQ.
即PC=CQ=DQ=$\frac{1}{2}$CD=$\frac{1}{2}$.
点评 本题考查了矩形的判定与性质,(1)利用了有一个角是直角的平行四边形是矩形,(2)利用了面积的分割,即矩形的面积减去4个三角形的面积等于小矩形的面积;(3)利用了正方形的性质:正方形的对角线垂直、相等且互相平分.

练习册系列答案
相关题目
1.计算(-x3)2的结果是( )
| A. | -x5 | B. | x5 | C. | -x6 | D. | x6 |
19.16的算术平方根是( )
| A. | ±4 | B. | -4 | C. | 4 | D. | ±8 |
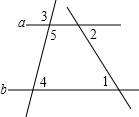 已知,如图所示,∠3=110°,∠4=70°,∠1=46°,求∠2的度数.
已知,如图所示,∠3=110°,∠4=70°,∠1=46°,求∠2的度数.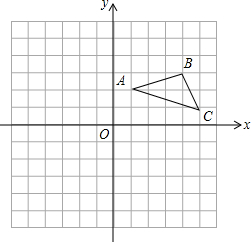 在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题:
在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题: 如图,AB是斜靠在墙角的长梯,梯角B距墙0.8m,长梯上一点D距墙0.7m,BD长0.55m,则梯子的长度是4.4m.
如图,AB是斜靠在墙角的长梯,梯角B距墙0.8m,长梯上一点D距墙0.7m,BD长0.55m,则梯子的长度是4.4m.
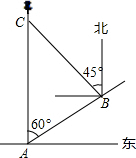 如图,一船在灯塔C的正南方向A处,上午10时,该船从A处沿北偏东60°方向航行,速度为20海里/时,中午13时到达B处,测得灯塔C在其北偏西45°方向上,试求此时船和灯塔的距离BC.
如图,一船在灯塔C的正南方向A处,上午10时,该船从A处沿北偏东60°方向航行,速度为20海里/时,中午13时到达B处,测得灯塔C在其北偏西45°方向上,试求此时船和灯塔的距离BC.