题目内容
14.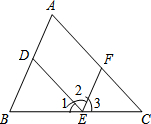 如图,在下列解答中,填空或填写适当的理由:
如图,在下列解答中,填空或填写适当的理由:(1)∵AB∥FE,( 已知 )
∴∠A=∠EFC,(两直线平行,同位角相等 )
∠2=∠BDE,(两直线平行,内错角相等 )
∠B+∠BEF=180°.(两直线平行,同旁内角互补 )
(2)∵∠2=∠EFC,(已知 )
∴AC∥DE.(内错角相等,两直线平行 )
(3)∵∠3=∠B,( 已知 )
∴AB∥EF.(同位角相等,两直线平行 )
分析 (1)直接根据平行线的性质可得出结论;
(2)、(3)根据平行线的判定定理可得出结论.
解答 解:(1)∵AB∥FE,( 已知 )
∴∠A=∠EFC,(两直线平行,同位角相等),
∠2=∠BDE,(两直线平行,内错角相等),
∠B+∠BEF=180°.(两直线平行,同旁内角互补).
故答案为:EFC,两直线平行,同位角相等;BDE,两直线平行,内错角相等;BEF,两直线平行,同旁内角互补;
(2)∵∠2=∠EFC,(已知),
∴AC∥DE.(内错角相等,两直线平行);
故答案为:EFC,内错角相等,两直线平行;
(3)∵∠3=∠B,(已知)
∴AB∥EF.(同位角相等,两直线平行).
故答案为:∠B;AB,EF,同位角相等,两直线平行.
点评 本题考查的是平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
4.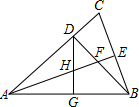 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )| A. | AH=2DF | B. | AF=2HE | C. | AF=2CE | D. | DH=DF |
19.16的算术平方根是( )
| A. | ±4 | B. | -4 | C. | 4 | D. | ±8 |
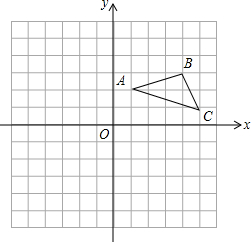 在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题:
在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题:
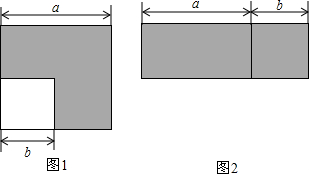 如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.
如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形. 在A、B、C、D四幅图案中,哪一幅可以通过平移(1)得到( )
在A、B、C、D四幅图案中,哪一幅可以通过平移(1)得到( )


