题目内容
11.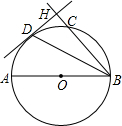 如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.
如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.(1)求证:DH是⊙O的切线;
(2)小强同学通过探究发现:BH+CH=AB,请你帮助小强同学证明这一结论.
分析 (1)要证明DH是⊙O的切线,只要证明OD⊥DH即可.
(2)通过证得RT△BDE≌RT△BDH、RTABDE≌RT△CDH得出BH=BE、HC=AE,即可证得结论.
解答  证明:连接OD,
证明:连接OD,
∵OB=OD,
∴∠ODB=∠OBD.
∵∠OBD=∠DBH,
∴∠ODB=∠DBH,
∴OD∥BH.
∵BH⊥DH,
∴OD⊥DH,
∴DH是⊙O的切线;
(2)过D作DE⊥AB于E,连接AD、DC,
∵BD平分∠ABH,DH⊥BH于点H,
∴DE=DH,
在RT△BDE和RT△BDH中,
$\left\{\begin{array}{l}{DE=DH}\\{BD=BD}\end{array}\right.$
∴RT△BDE≌RT△BDH(HL),
∴BH=BE,
∵∠ABD=∠CBD,
∴AD=DC,
在RT△ADE和RT△CDH中,
$\left\{\begin{array}{l}{DE=DH}\\{AD=DC}\end{array}\right.$
∴RTABDE≌RT△CDH(HL),
∴HC=AE,
∴BH+HC=BE+AE,
即BH+CH=AB.
点评 本题考查的是切线的判定、角平分线的性质、圆周角的性质、全等三角形的判定和性质,根据题意作出辅助线是解题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
1.计算(-x3)2的结果是( )
| A. | -x5 | B. | x5 | C. | -x6 | D. | x6 |
19.16的算术平方根是( )
| A. | ±4 | B. | -4 | C. | 4 | D. | ±8 |

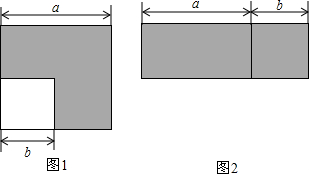 如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.
如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.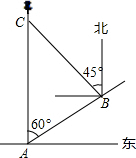 如图,一船在灯塔C的正南方向A处,上午10时,该船从A处沿北偏东60°方向航行,速度为20海里/时,中午13时到达B处,测得灯塔C在其北偏西45°方向上,试求此时船和灯塔的距离BC.
如图,一船在灯塔C的正南方向A处,上午10时,该船从A处沿北偏东60°方向航行,速度为20海里/时,中午13时到达B处,测得灯塔C在其北偏西45°方向上,试求此时船和灯塔的距离BC.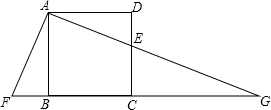 如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB延长线于点F,AE的延长线交BC的延长线于点G.若AF=7,DE=2,则EG的长是$\frac{21\sqrt{5}}{2}$-7.
如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB延长线于点F,AE的延长线交BC的延长线于点G.若AF=7,DE=2,则EG的长是$\frac{21\sqrt{5}}{2}$-7.