题目内容
17.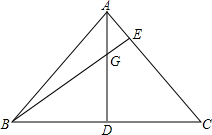 已知,AD⊥BC于点D,AD=BD,BE⊥AC于点E,BE交AD于点G,请说明:BG=AC.
已知,AD⊥BC于点D,AD=BD,BE⊥AC于点E,BE交AD于点G,请说明:BG=AC.
分析 先证出∠DBG=∠DAC,再由ASA证明△BDG≌△ADC,得出对应边相等即可.
解答 证明:∵AD⊥BC,BE⊥AC,
∴∠BDG=∠ADC=∠BEC=90°,
∴∠DBG+∠C=90°,∠DAC+∠C=90°,
∴∠DBG=∠DAC,
在△BDG和△ADC中,$\left\{\begin{array}{l}{∠BDG=∠ADC}&{\;}\\{BD=AD}&{\;}\\{∠DBG=∠DAC}&{\;}\end{array}\right.$,
∴△BDG≌△ADC(ASA),
∴BG=AC.
点评 本题考查了全等三角形的判定与性质、互余两角的关系;熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
7.若点P(x,y)在第一象限,则点Q(x+y,x-y)一定不在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第二、三象限 | D. | 第二、四象限 |
5.已知等腰三角形的两条边长分别是7和3.则下列四个数可作为第三条边长的是( )
| A. | 3 | B. | 4 | C. | 7 | D. | 7或3 |
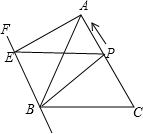 如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.
如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒. 在一次体育课上,体育老师对九年级一班的40名同学进行了立定跳远项目的测试,测试所得分数及相应的人数如图所示,这次测试的平均分为8.75分.
在一次体育课上,体育老师对九年级一班的40名同学进行了立定跳远项目的测试,测试所得分数及相应的人数如图所示,这次测试的平均分为8.75分. 如图,E,F分别为?ABCD的边AD,BC上的点,且AE=CF,AF与BE相交于点G,EC与DF相交于点H,猜想EF与GH之间的关系,并证明你的猜想.
如图,E,F分别为?ABCD的边AD,BC上的点,且AE=CF,AF与BE相交于点G,EC与DF相交于点H,猜想EF与GH之间的关系,并证明你的猜想.