题目内容
12.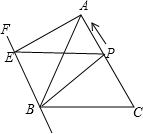 如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.
如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.(1)请用含t的代数式表示AP的长;
(2)当t为何值时,四边形BPAE为平行四边形,并说明理由;
(3)求出四边形BPAE的面积.
分析 (1)利用已知结合AP=AC-PC,进而得出答案;
(2)利用平行四边形的性质得出AP=BE,进而求出即可;
(3)利用梯形的面积求法得出四边形BPAE的面积=$\frac{1}{2}$(AP+BE)×BG进而求出即可.
解答 解:(1)由题意可得:CP=2t,AC=13cm,则AP=13-2t;
(2)当BE=AP时,四边形BPAE是平行四边形,
∵PE∥BC,BF∥AC,
∴四边形EBCP是平行四边形,
∴EB=PC,
即 2t=13-2t,
解得:t=$\frac{13}{4}$,
故t=$\frac{13}{4}$秒时,四边形BPAE为平行四边形;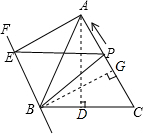
(3)过点A作AD⊥BC于点D,过点B作BP⊥AC于点G,
∵AB=AC=13cm,BC=10cm,
∴AD=12cm,则AD×BC=AC×BG,即12×10=13×BG,
解得:BG=$\frac{120}{13}$,
∵BE=2t,AP=13-2t,
∴AP+BE=13,
∴四边形BPAE的面积=$\frac{1}{2}$(AP+BE)×BG=$\frac{13}{2}$×$\frac{120}{13}$=60(cm2).
点评 此题主要考查了平行四边形的性质以及梯形面积求法和等腰三角形的性质,得出BG的长是解题关键.

练习册系列答案
相关题目
4. 如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
 如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{10}$ |
1.2014年德州市农村中小学校含标准化工程开工学校项目356个,开工面积56.2万平方米,开式面积量创历年最高,56.2万平方米用科学记数法表示正确的是( )
| A. | 5.62×104m2 | B. | 56.2×104m2 | C. | 5.62×105m2 | D. | 0.562×104m2 |
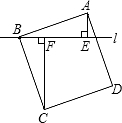 如图,过正方形ABCD的顶点B作直线l,过点A、C作l的垂线,垂足分别为点E、F,若AE=1,CF=2,求正方形的面积.
如图,过正方形ABCD的顶点B作直线l,过点A、C作l的垂线,垂足分别为点E、F,若AE=1,CF=2,求正方形的面积. 在平面直角坐标系中,点A是抛物线y=a(x-4)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为24.
在平面直角坐标系中,点A是抛物线y=a(x-4)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为24.
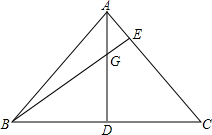 已知,AD⊥BC于点D,AD=BD,BE⊥AC于点E,BE交AD于点G,请说明:BG=AC.
已知,AD⊥BC于点D,AD=BD,BE⊥AC于点E,BE交AD于点G,请说明:BG=AC.