题目内容
5．已知等腰三角形的两条边长分别是7和3．则下列四个数可作为第三条边长的是（ ）| A． | 3 | B． | 4 | C． | 7 | D． | 7或3 |
分析 因为腰长与底边不确定，所以分①7为腰长，3为底边，②7为底边，3为腰长两种情况，再根据“三角形任意两边之和大于第三边，两边之差小于第三边”进行讨论．
解答 解：分两种情况讨论：
①当7为腰长，3为底边时，三边为7、7、3，能组成三角形，故第三边的长为7，
②当3为腰长，7为底边时，三边为7、3、3，3+3=6＜7，所以不能组成三角形．
因此第三边的长为7．
故选C．
点评 此题考查等腰三角形的性质，关键是本题利用三角形三边的关系求解，需要熟练掌握．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
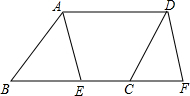在?ABCD中，点E在边BC上，点F在BC的延长线上，且EF=AD．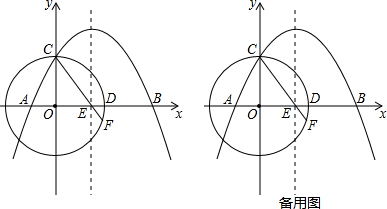
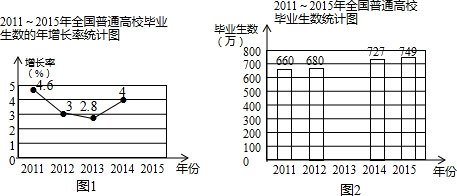
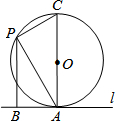如图，直线l与半径为6的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l于B点，连结AO并延长交⊙O于C点，连结PA、PC．①∠APC=90°度；②设PA=x，PB=y，则（x-y）的最大值是3．
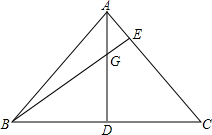已知，AD⊥BC于点D，AD=BD，BE⊥AC于点E，BE交AD于点G，请说明：BG=AC．
实数a、b、c在数轴上的对应点位置如图．化简：|c|-$\sqrt{（c+a）^{2}}$+$\sqrt{{b}^{2}}$-|a-b|．
15．
如图，数轴上所表示关于x的不等式组的解集是（ ）
如图，数轴上所表示关于x的不等式组的解集是（ ）| A． | x≥2 | B． | x＞2 | C． | x＞-1 | D． | -1＜x≤2 |