题目内容
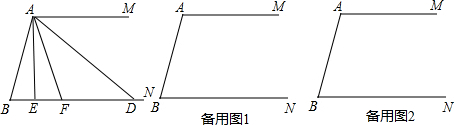
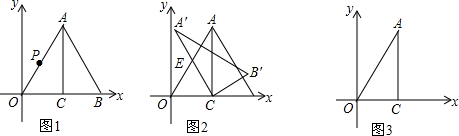
5.如图1,在平面直角坐标系中有一个Rt△OAC,其中∠ACO=90°,∠CAO=30°,OC=3,将该三角形沿直线AC翻折得到△BAC.(1)点A的坐标为(3,3$\sqrt{3}$),点B的坐标为(6,0),OA边所在直线的解析式为y=$\sqrt{3}$x;
(2)在图1中,一动点P从点O出发,沿折线O→A→B的方向以每秒2个单位的速度向B运动,设运动时间为t(秒).请求出当t为何值时,△ACP的面积为△AOB面积的$\frac{1}{3}$;
(3)如图2,固定△OAC,将△BAC绕点C逆时针旋转,旋转后得到△A′CB′,设A′C所在直线与OA所在直线的交点为E,请问在旋转过程中是否存在点E,使△ACE为等腰三角形?若存在,求出点E的坐标;若不存在,请说明理由.
分析 (1)根据勾股定理和折叠的性质易求得OA=AB=6,OB=6,AC=3$\sqrt{3}$,得到点A,B,的坐标,由点A,O的坐标用待定系数法求出OA解析式;
(2)点P在线段OA上运动,即0≤t≤3,以AC为底,PM=3-t为高,利用△ACP的面积为△AOB面积的$\frac{1}{3}$,建立方程求出t即可;
(3)设出点E(m,$\sqrt{3}$m)的坐标,分AC=AE.AC=CE,AE=CE三种情况建立方程求出m,即可求得符合条件的E点坐标.
解答 解:(1)∵∠ACO=90°,∠CAO=30°,OC=3
∴OA=6,AC=3$\sqrt{3}$,
∴A(3,3$\sqrt{3}$),
设直线OA解析式为y=kx,
∴3$\sqrt{3}$=3k,
∴k=$\sqrt{3}$,
∴直线OA解析式为y=$\sqrt{3}$x,
由对折有,OB=6,
∴B(6,0),
故答案为A(3,3$\sqrt{3}$),B(6,0),直线OA解析式为y=$\sqrt{3}$x,
(2)由题意知:OA=AB=6,OC=BC=3,OB=6;
∵AC⊥OB,AC=3$\sqrt{3}$,
∴S△AOB=$\frac{1}{2}$OB×AC=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$,
∴$\frac{1}{3}$S△AOB=3$\sqrt{3}$
∵△ACP的面积为△AOB面积的$\frac{1}{3}$,
∴点P只能在OA上,过点P作PM⊥AC,
∵OP=2t,
∴AP=6-2t,
∵0C=3,OA=6,
∵PM∥OC,
∴$\frac{AP}{AO}=\frac{PM}{OC}$,
∴$\frac{6-2t}{6}=\frac{PM}{3}$,
∴PM=3-t,
∴S△ACP=$\frac{1}{2}$AC×PM=$\frac{1}{2}$×3$\sqrt{3}$×(3-t),
∵△ACP的面积为△AOB面积的$\frac{1}{3}$,
∴$\frac{1}{2}$×3$\sqrt{3}$×(3-t)=3$\sqrt{3}$,
∴t=1,
(3)∵点E在直线OA上,设点E(m,$\sqrt{3}$m),
∵A(3,3$\sqrt{3}$),C(3,0),
∴AC=3$\sqrt{3}$,
∴AE=$\sqrt{(m-3)^{2}+(\sqrt{3}m-3\sqrt{3})^{2}}$=2|m-3|,
CE=$\sqrt{(m-3)^{2}+(\sqrt{3}m)^{2}}$=$\sqrt{4{m}^{2}-6m+9}$,
∵△ACE为等腰三角形,
①当AC=AE时,
∴2|m-3|=3$\sqrt{3}$,
∴m=3±$\frac{3\sqrt{3}}{2}$,
∴E1(3+$\frac{3\sqrt{3}}{2}$,3$\sqrt{3}$+$\frac{9}{2}$),E2(3-$\frac{3\sqrt{3}}{2}$,3$\sqrt{3}$-$\frac{9}{2}$)
②当AC=CE时,
∴$\sqrt{4{m}^{2}-6m+9}$=3$\sqrt{3}$,
∴m=3(舍)或m=-$\frac{3}{2}$,
∴E3(-$\frac{3}{2}$,-$\frac{3\sqrt{3}}{2}$),
③当AE=CE时,
∴2|m-3|=$\sqrt{4{m}^{2}-6m+9}$,
∴m=$\frac{3}{2}$,
∴E4($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),
∴存在点E,使△ACE为等腰三角形,满足条件的点E1(3+$\frac{3\sqrt{3}}{2}$,3$\sqrt{3}$+$\frac{9}{2}$),E2(3-$\frac{3\sqrt{3}}{2}$,3$\sqrt{3}$-$\frac{9}{2}$),E3(-$\frac{3}{2}$,-$\frac{3\sqrt{3}}{2}$),E4($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
点评 此题是几何变换综合题,主要考查了锐角三角函数,平面内,两点间的距离公式,三角形的面积计算方法,相似三角形的性质和判定,等腰三角形的性质,继而本题的关键是用时间t表示出线段,难点是分三种情况求点E的坐标,

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案 如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
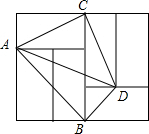 如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )
如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
| A. | ①②③④ | B. | ②③④ | C. | ②④ | D. | ②③ |
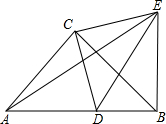 如图,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上-点.
如图,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上-点.