题目内容
12.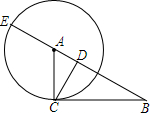 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据圆周角定理得到∠ECF=90°,得到∠ACE=∠FCB,根据等腰三角形的性质得到∠E=∠ACE,等量代换得到∠E=∠FCB,推出△BCE∽△BFC,根据相似三角形的性质得到$\frac{BC}{BE}=\frac{BF}{BC}$,推出BC2=BE•BF,由△ACB∽△BCD,根据相似三角形的性质得到$\frac{BC}{AB}=\frac{CD}{BC}$,于是得到BC2=BD•BA,等量代换得到BF•BE=BD•BA,同理得到CD2=DF•DE,由△ACD∽△BCD,得到$\frac{CD}{BD}=\frac{AD}{CD}$,于是得到CD2=AD•BD,即可得到结论.
解答 解:连接CF,CE,
∵EF是⊙O的直径,
∴∠ECF=90°,
∵∠BCA=90°,
∴∠ACE=∠FCB,
∵AE=AC,
∴∠E=∠ACE,
∴∠E=∠FCB,
∵∠B=∠B,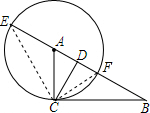
∴△BCE∽△BFC,
∴$\frac{BC}{BE}=\frac{BF}{BC}$,
∴BC2=BE•BF,
∵CD⊥AB,
∴∠ACB=∠BDC=90°,
∵∠B=∠B,
∴△ACB∽△BCD,
∴$\frac{BC}{AB}=\frac{CD}{BC}$,
∴BC2=BD•BA,
∴BF•BE=BD•BA,∴④正确,
同理△CDF∽△CDE,
∴$\frac{CD}{DE}=\frac{DF}{CD}$,
∴CD2=DF•DE,∴③正确,
∵∠ACB=90°,CD⊥AB,
∴△ACD∽△BCD,
∴$\frac{CD}{BD}=\frac{AD}{CD}$,
∴CD2=AD•BD,
∴①②错误,
故选B.
点评 本题考查了相似三角形的判定和性质,射影定理,圆周角定理,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
相关题目
1.化简-[-(x-y)]-[-(x+y)]可得( )
| A. | 2x | B. | 2x+2y | C. | 2y | D. | 2x-2y |
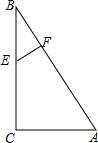 如图,在Rt△ABC中,∠C=90°,CA=$\frac{3}{4}$CB,点E在BC上,且BE=10,若EF⊥AB,求EF的长.
如图,在Rt△ABC中,∠C=90°,CA=$\frac{3}{4}$CB,点E在BC上,且BE=10,若EF⊥AB,求EF的长. 如图,△ABC中边BC=50,高AD=40,点E、F在AB、AC上,且EF∥BC交中线AM和高AD于点N和点G.
如图,△ABC中边BC=50,高AD=40,点E、F在AB、AC上,且EF∥BC交中线AM和高AD于点N和点G.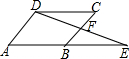 如图,AB∥CD,AD∥BC,E为AB延长线上一点,连结DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△BEF≌△CDF,你补充的条件是DC=BE(写一个即可).
如图,AB∥CD,AD∥BC,E为AB延长线上一点,连结DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△BEF≌△CDF,你补充的条件是DC=BE(写一个即可).