题目内容
3.解下列方程(1)2(6-4x)=2-6x
(2)$\frac{4x+1}{5}+\frac{3-x}{2}$-1=0.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号,得12-8x=2-6x,
移项,得-8x+6x=2-12,
合并同类项,得-2x=-10,
系数化为1,得x=5;
(2)去分母,得2(4x+1)+5(3-x)-10=0,
去括号,得8x+2+15-5x-10=0,
移项、合并同类项,得3x=-7,
系数化为1,得x=-$\frac{7}{3}$.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14. 如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )
如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )
 如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )
如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )| A. | 6m | B. | 8m | C. | 10m | D. | 12m |
11.将抛物线y=x2沿y轴向上平移一个单位后得到的新抛物线的解析式为( )
| A. | y=(x+1)2 | B. | y=(x-1)2 | C. | y=x2+1 | D. | y=x2-1 |
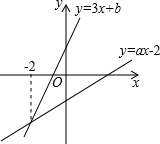 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.
如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.