题目内容
1.计算:(1)|-2|+($\frac{1}{3}$)-1×(π-$\sqrt{2}$)0-$\sqrt{9}$+(-1)2
(2)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$.
分析 (1)原式利用零指数幂、负整数指数幂法则,二次根式性质,绝对值的代数意义,以及乘方的意义计算即可得到结果;
(2)原式利用二次根式乘除法则计算,合并即可得到结果.
解答 解:(1)原式=2+3-3+1=3;
(2)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$=4-$\sqrt{6}$+2$\sqrt{6}$=4+$\sqrt{6}$.
点评 此题考查了二次根式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12. 如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
 如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )| A. | 63°30′ | B. | 53°30′ | C. | 73°30′ | D. | 93°30′ |
9. 实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )
实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )
 实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )
实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )| A. | A.-3a+b | B. | a+b | C. | -a+3b | D. | -a-b |
16.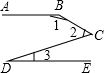 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )
 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=180° | C. | ∠1=∠2+∠3 | D. | ∠1-∠2+∠3=180° |
6. 如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )
如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )
 如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )
如图,等边△ABE的顶点E在正方形ABCD内,对角线AC和线段BE交于点F,若BA=$\sqrt{1+\sqrt{3}}$,则△ABF的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | 4-2$\sqrt{3}$ | D. | $\frac{1}{2}$+$\frac{\sqrt{3}}{4}$ |
13.若2m2-3m-7=0,7n2+3n-2=0,其中m,n为实数,且mn≠1,则m+$\frac{1}{n}$=( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{2}$ | D. | $-\frac{7}{2}$ |
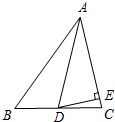 如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.
如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°. 如图,在正方形ABCD中,点E在BC上,以AE边作等腰Rt△AEF,∠AEF=90°,AE=EF,FG⊥BC于G.
如图,在正方形ABCD中,点E在BC上,以AE边作等腰Rt△AEF,∠AEF=90°,AE=EF,FG⊥BC于G.