题目内容
 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E是AD上一点,连接BE,CE,请找出图中所有相等的角,并说明理由.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E是AD上一点,连接BE,CE,请找出图中所有相等的角,并说明理由.考点:等腰三角形的性质
专题:
分析:先由AB=AC,根据等边对等角得出∠ABC=∠ACB;再由AB=AC,AD⊥BC,垂足为D,根据等腰三角形三线合一的性质及高的定义得出∠BAD=∠CAD,BD=DC,∠ADB=∠ADC=90°,则AD是BC的垂直平分线,根据线段垂直平分线的性质得到EB=EC,由等边对等角得出∠EBC=∠ECB,根据三角形内角和定理、邻补角定义及三角形外角的性质得出∠BED=∠CED,∠AEB=∠AEC,∠ABE=∠ACE.
解答:解:∠ABC=∠ACB;∠BAD=∠CAD;∠ADB=∠ADC;∠EBC=∠ECB;∠BED=∠CED;∠AEB=∠AEC;∠ABE=∠ACE.理由如下:
∵AB=AC,
∴∠ABC=∠ACB.
∵AB=AC,AD⊥BC,垂足为D,
∴∠BAD=∠CAD,BD=DC,∠ADB=∠ADC=90°,
∴AD是BC的垂直平分线,
∴EB=EC,
∴∠EBC=∠ECB,
∴∠BED=∠CED,∠AEB=∠AEC,∠ABE=∠ACE.
∵AB=AC,
∴∠ABC=∠ACB.
∵AB=AC,AD⊥BC,垂足为D,
∴∠BAD=∠CAD,BD=DC,∠ADB=∠ADC=90°,
∴AD是BC的垂直平分线,
∴EB=EC,
∴∠EBC=∠ECB,
∴∠BED=∠CED,∠AEB=∠AEC,∠ABE=∠ACE.
点评:本题考查了等腰三角形的性质,线段垂直平分线的性质,三角形的高的定义,三角形内角和定理,邻补角定义,三角形外角的性质等知识,综合性较强,但是难度不大,需认真仔细,以防漏解.

练习册系列答案
相关题目
 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,△OEB的面积为
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,△OEB的面积为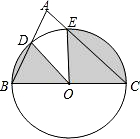 如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=72°,BC=4.求图中阴影部分的总周长和总面积(结果保留π)
如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=72°,BC=4.求图中阴影部分的总周长和总面积(结果保留π)