题目内容
16.在函数y=-$\frac{1}{x}$的图象上有三点(-3,y1),(-1,y2),(2,y3),则( )| A. | y3<y1<y2 | B. | y2<y3<y1 | C. | y3<y1<y2 | D. | y1<y2<y3 |
分析 根据反比例函数图象上点的坐标特征得到--3•y1=-1,-1•y2=-1,2•y3=-1,然后解方程求出y1,y2,y3,再比较它们的大小.
解答 解:根据题意得-3•y1=-1,-1•y2=-1,2•y3=-1,
解得y1=$\frac{1}{3}$,y2=1,y3=-$\frac{1}{2}$,
所以y3<y1<y2.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
6.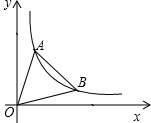 如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
 如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )| A. | 2$\frac{10}{11}$ | B. | 2$\frac{11}{12}$ | C. | 2$\frac{12}{13}$ | D. | 2$\frac{13}{14}$ |
4. 已知一次函数y=(a-1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a-1)x+b的图象如图所示,那么a的取值范围是( )
 已知一次函数y=(a-1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a-1)x+b的图象如图所示,那么a的取值范围是( )| A. | a<0 | B. | a>0 | C. | a>1 | D. | a<1 |
5.如下表是七年级某班5名同学数学测试成绩,根据信息完成下列问题:
①完成表中的空格信息;
②5人中最高分是谁?最低分是谁?分数与全班平均分最接近的是谁?
①完成表中的空格信息;
②5人中最高分是谁?最低分是谁?分数与全班平均分最接近的是谁?
| 姓名 | 王芳 | 刘兵 | 张昕 | 李聪 | 江文 |
| 成绩 | 89 | 92 | 90 | 84 | 88 |
| 与全班平 均分之差 | -1 | +2 | 0 | -6 | -2 |
6.在平面直角坐标系中,已知线段AB是两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为( )
| A. | (4,3) | B. | (3,-4) | C. | (3,4) | D. | (-2,-1) |
 如图,已知∠BOC=5∠AOC,OD平分∠AOB,且∠DOC=40°,求∠AOB的度数.
如图,已知∠BOC=5∠AOC,OD平分∠AOB,且∠DOC=40°,求∠AOB的度数. 如图,四边形ABCD内接于⊙O,若∠A=90°,则∠BCD的度数是90°.
如图,四边形ABCD内接于⊙O,若∠A=90°,则∠BCD的度数是90°.