题目内容
2.兴华初中准备购买10副某种品牌的乒乓球拍,每幅球拍配x(x≥2)个乒乓球,该校附近A,B两家超市都有这种品牌的乒乓球拍和乒乓球出售,且每副球拍的标价均为40元,每个乒乓球的标价为4元,目前两家超市同时在做促销活动:A超市:所有商品均打九折(按标价的90%)销售;
B超市:买一副乒乓球拍送2个乒乓球.
设在A超市购买乒乓球拍和乒乓球的费用为yA(元),在B超市购买乒乓球拍和乒乓球的费用为yB(元).请解答下列问题:
(1)分别写出yA、yB与x之间的关系式;
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
(3)若每副球拍配15个乒乓球,请你帮助该活动中心设计出最省钱的购买方案.
分析 (1)根据购买费用=单价×数量建立关系就可以表示出yA、yB的解析式;
(2)分三种情况进行讨论:当yA=yB时,当yA>yB时,当yA<yB时,分别求出购买划算的方案;
(3)分两种情况进行讨论计算求出需要的费用,再进行比较就可以求出结论.
解答 解:(1)由题意,得yA=(10×40+40x)×0.9=36x+360,yB=10×40+4(x-20)=4x+320.
(2)当yA=yB时,3.6x+360=4x+320,得x=100;
当yA>yB时,3.6x+360>4x+320,得x<100;
当yA<yB时,3.6x+360<4x+320,得x>100,
∴当2≤x<100时,到B超市购买划算,
当x=100时,两家超市一样划算,
当x>100时在A超市购买划算.
(3)由题意,知x=15×10=150>100,
∴选择A超市,yA=3.6×150+360=900(元);
如果先选择B超市购买10副乒乓球拍,送20个乒乓球,费用为400元,然后在A超市购买剩下的乒乓球,费用为(10×15-20)×4×0.9=468(元),共需费用868元.
∵868<900,
∴最佳方案是先选择在B超市购买10副乒乓球拍,然后在A超市购买130个乒乓球.
点评 本题考查了一次函数的解析式的运用,分类讨论的数学思想的运用,方案设计的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
7.小张在做数学题时,发现了下面有趣的结果:
3-2=1,
8+7-6-5=4,
15+14+13-12-11-10=9,
24+23+22+21-20-19-18-17=16,
…
根据以上规律可知,第20行左起第一个数是( )
3-2=1,
8+7-6-5=4,
15+14+13-12-11-10=9,
24+23+22+21-20-19-18-17=16,
…
根据以上规律可知,第20行左起第一个数是( )
| A. | 360 | B. | 339 | C. | 440 | D. | 483 |
14.抛物线y=ax2+bx+c经过点(4,-5)且对称轴是直线x=2,则代数式c-2的值为( )
| A. | 25 | B. | -25 | C. | $\frac{1}{25}$ | D. | -$\frac{1}{25}$ |
11.在下列实数中,为无理数的是( )
| A. | $\frac{1}{3}$ | B. | $\root{3}{-8}$ | C. | $\sqrt{4}$ | D. | $\sqrt{8}$ |
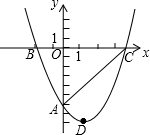 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.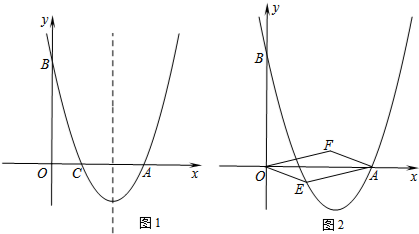
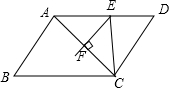 如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD、AC于E、F,连结CE,则△CDE的周长是10.
如图,已知AD∥BC,AB∥CD,AB=4,BC=6,EF是AC的垂直平分线,分别交AD、AC于E、F,连结CE,则△CDE的周长是10.