题目内容
19.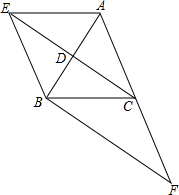 已知:如图,在△ABC中,CD是中线,过点A作BC的平行线交CD的延长线于点E,连接EB.
已知:如图,在△ABC中,CD是中线,过点A作BC的平行线交CD的延长线于点E,连接EB.(1)求证:AE=BC;
(2)延长AC到点F,使CF=AC,连接BF.当△ABF满足什么条件时,四边形AEBC是矩形?(写出你的猜想,并说明理由)
分析 (1)首先证明AD=BD,再根据平行线的性质可得∠EAB=∠CBA,然后再证明△AED≌△BCD可得AE=BC;
(2)当AB=BF时,四边形AEBC是矩形;根据AE=BC,AE∥BC,可证明四边形ACBE是平行四边形,再由等腰三角形的性质可得CB⊥AF,根据有一个角是直角的平行四边形是矩形可得结论.
解答 (1)证明:∵CD是中线,
∴AD=BD,
∵AE∥BC,
∴∠EAB=∠CBA,
在△AED和△BCD中,$\left\{\begin{array}{l}{∠EAD=∠CBD}\\{AD=BD}\\{∠ADE=∠BDC}\end{array}\right.$,
∴△AED≌△BCD(ASA),
∴AE=BC;
(2)解:当AB=BF时,四边形AEBC是矩形,
∵AE=BC,AE∥BC,
∴四边形ACBE是平行四边形,
∵AB=BF,AC=CF,
∴CB⊥AF,
∴∠ACB=90°,
∴四边形AEBC是矩形.
点评 此题主要考查了矩形的判定,以及全等三角形的判定和性质,关键是掌握有一个角是直角的平行四边形是矩形.

练习册系列答案
相关题目
11.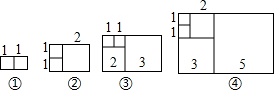 如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
 如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )
如图矩形都是由大小不等的正方形按照一定规律组成的,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…,则第⑧个矩形的周长为( )| A. | 168 | B. | 170 | C. | 178 | D. | 188 |
8. 如图这个立体图形的俯视图正确的是( )
如图这个立体图形的俯视图正确的是( )
 如图这个立体图形的俯视图正确的是( )
如图这个立体图形的俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
9.下列图形中,把△ABC平移后,能得到△DEF的是( )
| A. |  | B. |  | C. |  | D. |  |
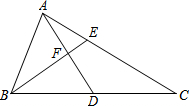 已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=8,BF=5,则AC的长等于13.
已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=8,BF=5,则AC的长等于13.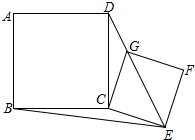 将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$.
将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$.