题目内容
12. 如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( )
如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( )| A. | P是BC中点 | B. | ∠APE=90° | C. | ∠APB=∠EPC | D. | BP:BC=2:3 |
分析 由四边形ABCD是正方形,可得∠B=∠C=90°,又由E是CD的中点,易得CE:AB=1:2,然后分别利用相似三角形的判定定理,判定△ABP与△ECP相似.
解答 解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=CD=BC,
∵E是CD的中点,
∴CD:CD=1:2,
即CE:AB=1:2,
A、∵P是BC中点,
∴BP=PC=$\frac{1}{2}$BC,
没办法判定:△ABP与△ECP中各边成比例;故错误;
B、∵∠APE=90°,
∴∠APB+∠CPE=90°,
∵∠BAP+∠APB=90°,
∴∠BAP=∠CPE,
∴△ABP∽△PCE;故正确;
C、∵∠APB=∠EPC,
∴△ABP∽△EPC,故正确;
D、∵BP:BC=2:3,
∴PC:BP=1:2,
∴PC:BP=CE:AB=1:2,
∴△ABP∽△PCE,故正确.
故选A.
点评 此题考查了相似三角形的判定以及正方形的性质.注意灵活应用判定定理是关键.

练习册系列答案
相关题目
3.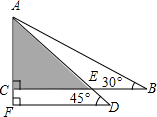 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.| A. | 14 | B. | 24.5 | C. | 7 | D. | 49 |
7.抛物线y=-3(x-1)2-2的开口方向、对称轴和顶点坐标是( )
| A. | 开口向上,对称轴为直线x=-1,顶点(-1,-2) | |
| B. | 开口向上,对称轴为直线x=1,顶点(1,-2) | |
| C. | 开口向下,对称轴为直线x=-1,顶点(1,2) | |
| D. | 开口向下,对称轴为直线x=1,顶点(1,-2) |
17.下列语句不是命题的是( )
| A. | 两点之间线段最短 | B. | 过点P作线段AB的垂直平分线 | ||
| C. | 不平行的两条直线有一个交点 | D. | 对顶角不相等 |
2.函数y=(k2+2k)xk2+k-1是反比例函数,则k的值为( )
| A. | 1 | B. | -1 | C. | 0或-1 | D. | ±1 |
 已知P(-3,m)和 Q(1,m)是抛物线y=x2+bx-3上的两点.
已知P(-3,m)和 Q(1,m)是抛物线y=x2+bx-3上的两点.