题目内容
4．（1）（3x-2）（x-3）-2（x+6）（x-3）（2）（x+2y-3z）（x-2y+3z）
分析 （1）利用多项式乘多项式的计算方法计算，进一步合并得出答案即可；
（2）先利用平方差公式计算，再利用完全平方公式计算即可．
解答 解：（1）原式=3x2-9x-2x+6-2x2+6x-12x+36
=x2-17x+42；
（2）原式=[x+（2y-3z）][x-（2y-3z）]
=x2-（2y-3z）2
=x2-4y2+12yz+9z2．
点评 此题考查整式的混合运算，掌握计算方法和合并同类项的方法是解决问题的关键．
练习册系列答案
相关题目
12．
如图，ABCD是正方形，E是CD的中点，P是BC边上的一点，下列条件中，不能推出△ABP与△ECP相似的是（ ）
如图，ABCD是正方形，E是CD的中点，P是BC边上的一点，下列条件中，不能推出△ABP与△ECP相似的是（ ）| A． | P是BC中点 | B． | ∠APE=90° | C． | ∠APB=∠EPC | D． | BP：BC=2：3 |
9．
如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC．下列比例式正确的是（ ）
如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC．下列比例式正确的是（ ）| A． | $\frac{AD}{DB}$=$\frac{CE}{AE}$ | B． | $\frac{AD}{DB}$=$\frac{AE}{AC}$ | C． | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | D． | $\frac{AD}{AB}$=$\frac{EC}{AE}$ |
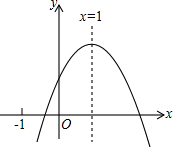二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为x=1，有下列结论：
如图，在△ABC中，∠ADE=∠C，AE=3，AB=6，AD=2.4，则AC=4.8．