题目内容
19.已知:一条动直线y═mx+n与双曲线y=$\frac{k}{x}$(k>0)交于点A(a,b)和点B(-b,-a),且b>a>0,若直线y=mx+n与y轴交于点C,点O是原点,且△AOC的面积为$\frac{k}{2}-\frac{2}{{b}^{2}}$,求双曲线的解析式.分析 过点A作AE⊥y轴于点E,由点A、B的坐标结合直线AB的解析式即可得出n=b-a,将x=0代入直线AB的解析式中即可求出点C的坐标,从而得出CE的长,再根据三角形的面积、反比例函数系数k的几何意义结合反比例函数图象上点的坐标特征即可得出a2•b2=(ab)2=k2=4,解之即可得出k值,此题得解.
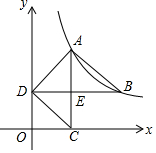
解答 解:过点A作AE⊥y轴于点E,如图所示.
∵点A(a,b)和点B(-b,-a)在直线y═mx+n上,
∴$\left\{\begin{array}{l}{b=am+n}\\{-a=-bm+n}\end{array}\right.$,解得:n=b-a.
当x=0时,y=mx+n=n=b-a,
∴点C(0,b-a),
∴CE=b-(b-a)=a,
∴S△AOC=S△AOE-S△ACE=$\frac{k}{2}$-$\frac{1}{2}$AE•CE=$\frac{k}{2}$-$\frac{1}{2}$a•a=$\frac{k}{2}-\frac{2}{{b}^{2}}$,
∴a2•b2=(ab)2=k2=4,
解得:k=2或k=-2(舍去).
∴双曲线的解析式为y=$\frac{2}{x}$.
点评 本题考查了反比例函数与一次函数的交点问题、三角形的面积、反比例函数系数k的几何意义以及反比例函数图象上点的坐标特征,根据三角形的面积、反比例函数系数k的几何意义结合反比例函数图象上点的坐标特征找出(ab)2=k2=4是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.计算(x+2)2,正确的是( )
| A. | x2+4 | B. | x2+2 | C. | x2+4x+4 | D. | 2x+4 |
8.济南园博园对2016年国庆黄金周七天假期的游客人数进行了统计,如表:
其中平均数和中位数分别是( )
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 旅游人数(万) | 1.5 | 2.2 | 2.2 | 3.8 | 1.5 | 2.2 | 0.6 |
| A. | 2和2.2 | B. | 2和2 | C. | 1.5和2.2 | D. | 2.2和3.8 |




 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.