题目内容
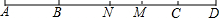 如图,AC=BD,BC:AD=5:9,M是BD的中点.
如图,AC=BD,BC:AD=5:9,M是BD的中点.(1)若CM=6cm,求AD的长.
(2)若N是AD的中点,且MN=6cm,求AD的长.
考点:两点间的距离
专题:
分析:(1)利用已知结合AC=BD,BC:AD=5:9,进而用未知数表示出各线段长,进而求出答案;
(2)利用已知结合AC=BD,BC:AD=5:9,进而用未知数表示出各线段长,进而求出答案.
(2)利用已知结合AC=BD,BC:AD=5:9,进而用未知数表示出各线段长,进而求出答案.
解答: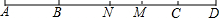 解:(1)∵AC=BD,
解:(1)∵AC=BD,
∴AB+BC=BC+CD,
∴AB=DC,
∵BC:AD=5:9,
∴设BC=5x,AD=9x,则AB=DC=2x,
故BD=5x+2x=7x,
∵M是BD的中点,
∴BM=DM=3.5x,故MC=1.5x,
∵CM=6cm,
∴1.5x=6,
解得:x=4,
∴AD的长为:9×4=36(cm);
(2)由(1)得:设BC=5x,AD=9x,
则AB=DC=2x,
故BD=5x+2x=7x,
∵M是BD的中点,
∴BM=DM=3.5x,故MC=1.5x,
∵N是AD的中点,
∴DN=4.5x,
∴MN=4.5x-2x-1.5x=x,
∵MN=6cm,
∴x=6,
∴AD的长为:6×9=54(cm).
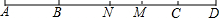 解:(1)∵AC=BD,
解:(1)∵AC=BD,∴AB+BC=BC+CD,
∴AB=DC,
∵BC:AD=5:9,
∴设BC=5x,AD=9x,则AB=DC=2x,
故BD=5x+2x=7x,
∵M是BD的中点,
∴BM=DM=3.5x,故MC=1.5x,
∵CM=6cm,
∴1.5x=6,
解得:x=4,
∴AD的长为:9×4=36(cm);
(2)由(1)得:设BC=5x,AD=9x,
则AB=DC=2x,
故BD=5x+2x=7x,
∵M是BD的中点,
∴BM=DM=3.5x,故MC=1.5x,
∵N是AD的中点,
∴DN=4.5x,
∴MN=4.5x-2x-1.5x=x,
∵MN=6cm,
∴x=6,
∴AD的长为:6×9=54(cm).
点评:此题主要考查了两点之间的距离,利用未知数表示出各边长是解题关键.

练习册系列答案
相关题目
要使分式
有意义,x的取值范围为( )
| ||
| x+5 |
| A、x≠-5 | B、x>0 |
| C、x≠-5且x>0 | D、x≥0 |
在直角坐标系xOy中,一次函数y=
x+1的图象与二次函数y=-x2+
x+1的图象交于点A、B,则锐角∠ABO的正弦值等于( )
| 1 |
| 2 |
| 9 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=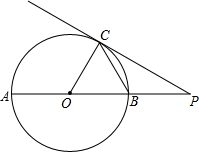 如图,P是⊙O直径AB延长线上的一点,PC切⊙O于点C,∠P=30°,⊙O的半径长为6.
如图,P是⊙O直径AB延长线上的一点,PC切⊙O于点C,∠P=30°,⊙O的半径长为6.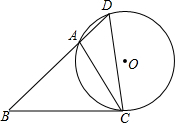 如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆
如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.