Question

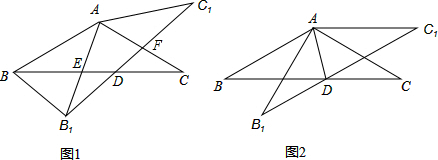
11．如图1，在等腰△ABC中，∠BAC=120°，将△ABC绕点A逆时针旋转角α．（0°＜α＜60°）得到△A₁B₁C，连结BB₁，AB₁交BC于E点，B₁C₁分别交BC、AC于D、F两点．
（1）在图中不再添加其它任何线段的情况下，请你找出两对全等的三角形，并选择其中的一对予以证明（△ABC与△A₁B₁C₁全等除外）；
（2）当BE=BB₁时，求此时旋转角α的度数；
（3）如图2，连结AD，当C₁A=C₁D时，判断此时四边形ABDC₁的形状．

Answer 1

分析 （1）根据等腰三角形性质和三角形内角和定理，求出∠ABC=∠ACB=∠C₁=∠AB₁C₁=30°，求出∠BAE=∠C₁AF，根据ASA推出△ABE≌△AC₁F，由此可得AE=AF，根据SAS即可得出△AEC≌△AFB₁；
（2）由旋转可得，∠BAB₁=α，AB=AB₁，根据等腰三角形ABB₁，求得∠BB₁E=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α，根据三角形外角性质，求得∠BEB₁=∠ABE+∠BAE=30°+α，而当BE=BB₁时，∠BEB₁=∠BB₁E，据此列出方程30°+α=90°-$\frac{1}{2}$α，解得α=40°即可；
（3）先过点A作AG⊥B₁C₁于G，过点A作AH⊥BC于H，根据全等三角形的性质，得出AH=AG，进而得出AD平分∠BDC₁，再根据△ADC₁是等腰三角形，求得∠ADC₁=∠DAC₁=75°，进而得出∠BDC₁=2×75°=150°，最后判定AC₁∥BC，AB∥C₁D，得出四边形ABDC₁是平行四边形，进而得出四边形ABDC₁是菱形．

解答 解：（1）图中存在两对全等的三角形：△ABE≌△AC₁F，△AEC≌△AFB₁；
选择前一对，证明如下：
∵△ABC中，AB=AC，∠BAC=120°，
∴∠ABC=∠ACB=∠C₁=∠AB₁C₁=30°，
∵∠BAC=∠B₁AC₁=120°，
∴∠BAE=∠C₁AF，
在△ABE和△AC₁F中，
$\left\{\begin{array}{l}{∠ABE=∠{C}_{1}}\\{AB=A{C}_{1}}\\{∠BAE=∠FA{C}_{1}}\end{array}\right.$，
∴△ABE≌△AC₁F（ASA）；

（2）当BE=BB₁时，∠BEB₁=∠BB₁E，
由旋转可得，∠BAB₁=α，AB=AB₁，
∴等腰三角形ABB₁中，∠BB₁E=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α，
∵∠BEB₁是△ABE的外角，
∴∠BEB₁=∠ABE+∠BAE=30°+α，
∴30°+α=90°-$\frac{1}{2}$α，
解得α=40°，
∴旋转角α的度数为40°；

（3）四边形ABDC₁是菱形．
过点A作AG⊥B₁C₁于G，过点A作AH⊥BC于H，
∵△ABC与△A₁B₁C₁全等，
∴BC=B₁C₁，△ABC与△A₁B₁C₁面积相等，
∴AH=AG，
又∵AG⊥B₁C₁，AH⊥BC，
∴AD平分∠BDC₁，
当C₁A=C₁D时，△ADC₁是等腰三角形，
∵∠C₁=30°，
∴∠ADC₁=∠DAC₁=75°，
∴∠BDC₁=2×75°=150°，
∴∠BDC₁+∠B=150°+30°=180°，∠BDC₁+∠C₁=150°+30°=180°，
∴AC₁∥BC，AB∥C₁D，
∴四边形ABDC₁是平行四边形，
∵C₁A=C₁D，
∴四边形ABDC₁是菱形．

点评 本题主要考查了等腰三角形的性质、全等三角形的判定与性质、平行四边形与菱形的判定等，解决问题的关键是掌握全等三角形的判定方法与菱形的判定方法，解题时注意方程思想的运用和角平分线的性质定理的逆定理的运用．