题目内容
5.在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验.发现摸到白球的频率稳定在0.75,则n的值为6;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,求摸出的2个球颜色不同的概率.
分析 (1)根据白球的频率稳定在0.75附近得到白球的概率约为0.75,根据白球个数确定出总个数,进而确定出黑球个数;
(2)将所有等可能的结果列举出来,利用概率公式求解即可.
解答 解:(1)根据题意得:$\frac{n}{n+2}$=0.75,
解得:n=6,
则n的值为6,
故答案为:6;
(2)任意摸出2个球,共有12种等可能的结果,即(红,绿)、(红,白1)、(红,白2)、(绿,红)、(绿,白1)、(绿,白1)、(白1,红)、(白1,绿)、(白1,白2)、(白2,红)、(白2,绿)、(白2,白1),
其中2个球颜色不同的结果有10种,所以所求概率为$\frac{5}{6}$.
点评 此题考查了利用频率估计概率,解答此题的关键是了解白球的频率稳定在0.75附近即为概率约为0.75.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,AD是Rt△ABC斜边上的高.若AB=4cm,BC=10cm,则BD=1.6cm.
如图,AD是Rt△ABC斜边上的高.若AB=4cm,BC=10cm,则BD=1.6cm.
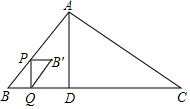 如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).