题目内容
如图，AF与BE互相平分，EC与DF互相平分，求证：四边形ABCD是平行四边形．考点：平行四边形的判定
专题：证明题
分析：连接AE、DE、EF、BF、CF，根据AF与BE互相平分，EC与DF互相平分，得到四边形AEFB和四边形EFCD是平行四边形，从而得到AB∥CD，AB=CD，利用一组对边平行且相等的四边形是平行四边形判定四边形ABCD是平行四边形即可．
解答：
证明：连接AE、DE、EF、BF、CF，
∵AF与BE互相平分，EC与DF互相平分，
∴四边形AEFB和四边形EFCD是平行四边形，
∴AB∥EF∥CD，AB=EF=CD，
∴AB∥CD，AB=CD，
∴四边形ABCD是平行四边形．
证明：连接AE、DE、EF、BF、CF，∵AF与BE互相平分，EC与DF互相平分，
∴四边形AEFB和四边形EFCD是平行四边形，
∴AB∥EF∥CD，AB=EF=CD，
∴AB∥CD，AB=CD，
∴四边形ABCD是平行四边形．
点评：本题考查了平行四边形的判定，解题的关键是正确的作出辅助线，并利用平行四边形的判定定理进行判定．
练习册系列答案
阅读快车系列答案
相关题目
一个山坡的倾斜角为10°，坡上有一棵树AB，当阳光与水平线成50°角时，树影BC的长为6米，求树高AB．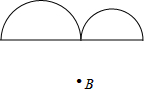
画出如图所示的两个半圆关于点B成中心对称的图形．
如图，直线AP的解析式y=kx+4k分别交于x轴、y轴于A、C两点，与反比例函数y=
如图，已知∠3+∠DCB=180°，∠1=∠2，∠CME：∠GEM=4：5，求∠CME的度数．