题目内容
利用平方差公式计算:
(1)(1+
)×(1+
)×(1+
)×(1+
)×(1+
)
(2)1002-992+982-972+962-952+22-12.
(1)(1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 28 |
| 1 |
| 216 |
(2)1002-992+982-972+962-952+22-12.
考点:平方差公式
专题:计算题
分析:(1)添上2×(1-
),再依次运用平方差公式求出即可;
(2)根据平方差公式分解,最后合并即可.
| 1 |
| 2 |
(2)根据平方差公式分解,最后合并即可.
解答:解:(1)原式=2×(1-
))(1+
)×(1+
)×(1+
)×(1+
)×(1+
)
=2×(1-
)×(1+
)×(1+
)×(1+
)×(1+
)
=2×(1-
)×(1+
)×(1+
)×(1+
)
=2×(1-
)×(1+
)×(1+
)
=2×(1-
)×(1+
)
=2×(1-
)
=2-
.
(2)原式=1002-992+982-972+962-952+22-12
=(100+99)×(100-99)+(98+97)×(98-97)+(2+1)×(2-1)
=199+195+3
=397.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 28 |
| 1 |
| 216 |
=2×(1-
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 28 |
| 1 |
| 216 |
=2×(1-
| 1 |
| 24 |
| 1 |
| 24 |
| 1 |
| 28 |
| 1 |
| 216 |
=2×(1-
| 1 |
| 28 |
| 1 |
| 28 |
| 1 |
| 216 |
=2×(1-
| 1 |
| 216 |
| 1 |
| 216 |
=2×(1-
| 1 |
| 232 |
=2-
| 1 |
| 231 |
(2)原式=1002-992+982-972+962-952+22-12
=(100+99)×(100-99)+(98+97)×(98-97)+(2+1)×(2-1)
=199+195+3
=397.
点评:本题考查了平方差公式的应用,主要考查学生运用公式进行推理和计算的能力.

练习册系列答案
相关题目
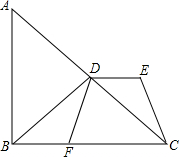 在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状.
在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状. 如图,AF与BE互相平分,EC与DF互相平分,求证:四边形ABCD是平行四边形.
如图,AF与BE互相平分,EC与DF互相平分,求证:四边形ABCD是平行四边形.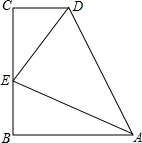 如图,在梯形ABCD中,AB∥CD,E是BC的中点,AB+CD=AD,求证:
如图,在梯形ABCD中,AB∥CD,E是BC的中点,AB+CD=AD,求证: