题目内容
某公司生产并销售A,B两种品牌新型节能设备,第一季度共生产两种品牌设备20台,每台的成本和售价如下表:
设销售A种品牌设备x台,20台A,B两种品牌设备全部售完后获得利润y万元.(利润=销售价-成本)
(1)求y关于x的函数关系式;
(2)若生产两种品牌设备的总成本不超过80万元,那么公司如何安排生产A,B两种品牌设备,售完后获利最多?并求出最大利润;
(3)公司为营销人员制定奖励促销政策:第一季度奖金=公司总利润×销售A种品牌设备台数×1%,那么营销人员销售多少台A种品牌设备,获得奖励最多?最大奖金数是多少?
| 品牌 | A | B |
| 成本价(万元/台) | 3 | 5 |
| 销售价(万元/台) | 4 | 8 |
(1)求y关于x的函数关系式;
(2)若生产两种品牌设备的总成本不超过80万元,那么公司如何安排生产A,B两种品牌设备,售完后获利最多?并求出最大利润;
(3)公司为营销人员制定奖励促销政策:第一季度奖金=公司总利润×销售A种品牌设备台数×1%,那么营销人员销售多少台A种品牌设备,获得奖励最多?最大奖金数是多少?
考点:二次函数的应用
专题:销售问题,优选方案问题
分析:(1)设销售A种品牌设备x台,B种品牌设备(20-x)台,算出每台的利润乘对应的台数,再合并在一起即可求出总利润;
(2)由“生产两种品牌设备的总成本不超过80万元”,列出不等式,再由(1)中的函数的性质得出答案;
(3)利用“第一季度奖金=公司总利润×销售A种品牌设备台数×1%”,列出二次函数,利用配方法求得最大值即可.
(2)由“生产两种品牌设备的总成本不超过80万元”,列出不等式,再由(1)中的函数的性质得出答案;
(3)利用“第一季度奖金=公司总利润×销售A种品牌设备台数×1%”,列出二次函数,利用配方法求得最大值即可.
解答:解:(1)y=(4-3)x+(8-5)×(20-x),
即y=-2x+60(0≤x≤20).
(2)3x+5×(20-x)≤80,
解得x≥10.
结合(1)可知,当x=10时,y最大=40万元.
故公司生产A,B两种品牌设备各10台,售完后获利最大,最大利润为40万元.
(3)设营销人员第一季度奖金为w,则w=xy×1%,
即w=x(-2x+60)×1%=-
(x-15)2+4.5,
故当x=15时,w取最大值,为4.5.
故营销人员销售15台A种品牌设备,获得第一季度奖金最多,最大奖金数为4.5万元.
即y=-2x+60(0≤x≤20).
(2)3x+5×(20-x)≤80,
解得x≥10.
结合(1)可知,当x=10时,y最大=40万元.
故公司生产A,B两种品牌设备各10台,售完后获利最大,最大利润为40万元.
(3)设营销人员第一季度奖金为w,则w=xy×1%,
即w=x(-2x+60)×1%=-
| 1 |
| 50 |
故当x=15时,w取最大值,为4.5.
故营销人员销售15台A种品牌设备,获得第一季度奖金最多,最大奖金数为4.5万元.
点评:此题综合考查二次函数、一次函数、不等式的应用,注意题目蕴含的数量关系,正确列式解决问题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
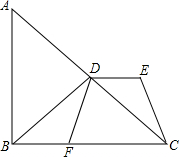 在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状.
在Rt△ABC中,BD是斜边AC的中线,DE∥BF,且DE=BF,试判定四边形DECF的形状. 如图,AF与BE互相平分,EC与DF互相平分,求证:四边形ABCD是平行四边形.
如图,AF与BE互相平分,EC与DF互相平分,求证:四边形ABCD是平行四边形.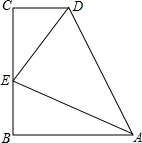 如图,在梯形ABCD中,AB∥CD,E是BC的中点,AB+CD=AD,求证:
如图,在梯形ABCD中,AB∥CD,E是BC的中点,AB+CD=AD,求证: 如图,四边形ABCD是正方形,点G是BC上任意一点,BE⊥AG于点E,点F为AE上一点,且AE-BE=EF,求证:BE∥DF.
如图,四边形ABCD是正方形,点G是BC上任意一点,BE⊥AG于点E,点F为AE上一点,且AE-BE=EF,求证:BE∥DF. 如图,一艘货轮由港口A出发向正东方向行驶,在港口A处时,测得灯塔B在港口A的南偏东30°方向,小岛C在港口A的南偏东60°方向,当这艘货轮行驶60海里到点D处时,小岛C恰好在点D处的正南方向,此时测得灯塔B在南偏西60°的方向,求:
如图,一艘货轮由港口A出发向正东方向行驶,在港口A处时,测得灯塔B在港口A的南偏东30°方向,小岛C在港口A的南偏东60°方向,当这艘货轮行驶60海里到点D处时,小岛C恰好在点D处的正南方向,此时测得灯塔B在南偏西60°的方向,求: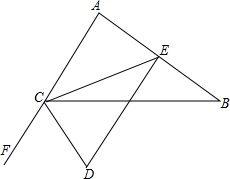 如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.
如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.