题目内容
一个山坡的倾斜角为10°，坡上有一棵树AB，当阳光与水平线成50°角时，树影BC的长为6米，求树高AB．考点：解直角三角形的应用-坡度坡角问题
专题：几何图形问题
分析：应充分利用所给的10°和50°在树的位置构造直角三角形，进而利用三角函数求解．
解答：
解：如图，过点C作水平线与AB的延长线交于点D，则AD⊥CD，
∴∠BCD=10°，∠ACD=50°．
在Rt△CDB中，CD=6cos10°，BD=6sin10°，
在Rt△CDA中，AD=CDtan50°=6cos10°•tan50°，
∴AB=AD-BD
=（6cos15°•tan50°-6sin10°）
=6（cos10°•tan50°-sin10°）m．
答：树高AB为6（cos10°•tan50°-sin10°）m．
解：如图，过点C作水平线与AB的延长线交于点D，则AD⊥CD，∴∠BCD=10°，∠ACD=50°．
在Rt△CDB中，CD=6cos10°，BD=6sin10°，
在Rt△CDA中，AD=CDtan50°=6cos10°•tan50°，
∴AB=AD-BD
=（6cos15°•tan50°-6sin10°）
=6（cos10°•tan50°-sin10°）m．
答：树高AB为6（cos10°•tan50°-sin10°）m．
点评：本题考查锐角三角函数的应用．需注意构造直角三角形是常用的辅助线方法．
练习册系列答案
相关题目
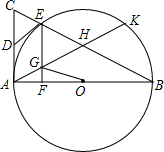在Rt△ABC中，∠BAC=90°，以AB为直径⊙O交BC于点E，D为AC中点，EF⊥AB于点F．过A作AK∥DE交⊙O于K，交BC于H，交EF于G．
如图，BE、BD是△ABC中∠ABC的内、外角平分线，AD⊥BD于D，AE⊥BE于E，交BC的延长线于F．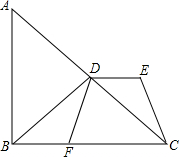
在Rt△ABC中，BD是斜边AC的中线，DE∥BF，且DE=BF，试判定四边形DECF的形状．
如图，AF与BE互相平分，EC与DF互相平分，求证：四边形ABCD是平行四边形．
如图，一艘货轮由港口A出发向正东方向行驶，在港口A处时，测得灯塔B在港口A的南偏东30°方向，小岛C在港口A的南偏东60°方向，当这艘货轮行驶60海里到点D处时，小岛C恰好在点D处的正南方向，此时测得灯塔B在南偏西60°的方向，求：