题目内容

19．若x1与x2的平均数为6，则x1+1与x2+3的平均数为8．

分析 根据平均数的性质知，要求x1+1，x2+3平均数，只要把数x1、x2的和表示出即可．

解答 解：∵数x1、x2的平均数为6，
∴数x1+x2=2，6=12，
∴x1+1、x2+3的平均数
=（x1+1+x2+3）÷2
=（12+4）÷2
=16÷2
=8．
故答案为8．

点评 本题考查的是样本平均数的求法．解决本题的关键是用一组数据的平均数表示另一组数据的平均数．

练习册系列答案
相关题目
9．如图，菱形ABCD中，AB=2，∠C=60°，我们把菱形ABCD的对称中心O称作菱形的中心，菱形ABCD在直线L上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫做一次操作，则经过2013次这样的操作菱形中心O所经过的路径总长为（　　）
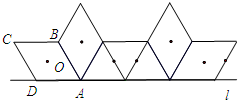
A．$\frac{{671（\sqrt{3}+1）}}{3}$πB．$\frac{{671（2\sqrt{3}+1）}}{2}$πC．$\frac{{671（2\sqrt{3}+1）}}{3}$πD．$\frac{{1342\sqrt{3}}}{3}$π
10．下列函数中，是二次函数的是（　　）
A．y=-3xB．y=$\frac{4}{x}$C．y=-2x-1D．y=2x2
7．解下列方程
（1）x2-2x-3=0
（2）（2x-1）2=（3-x）2．
14．（1）$\sqrt{12}$-$\frac{1}{2-\sqrt{3}}$+1         
（2）$\sqrt{27}$+|7|+（$\frac{1}{\sqrt{5}-1}$）0+（$\frac{1}{2}$）-1．
4．已知a=3+$\sqrt{5}$，b=3-$\sqrt{5}$，则代数式$\sqrt{{a^2}-ab+{b^2}}$的值是（　　）
A．24B．±2$\sqrt{6}$C．2$\sqrt{6}$D．2$\sqrt{5}$
11．下列各式计算正确的是（　　）
A．-2a+5b=3abB．6a+a=6a2C．4m2n-2mn2=2mnD．3ab2-5b2a=-2ab2
8．下列各式中不能使用平方差公式的是（　　）
A．（a+b）（a-b）B．（-a+b）（b-a）C．（-a+b）（-b-a）D．（a-b）（-a-b）
9．如果|a+3|+（b-2）2=0，那么代数式（a+b）2013的值是（　　）
A．-2013B．2013C．-1D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网