题目内容
14.一批货物要运往某地,货主准备租用甲、乙两种货车,过去两次租用这种货车的情况如下表:| 第一次 | 第二次 | |
| 甲种货车辆数(辆) | 2 | 5 |
| 乙种货车辆数(辆) | 3 | 6 |
| 累计运货吨数(吨) | 15.5 | 35 |
分析 表中的数值都和甲种货车和乙种货车的载重量有关,所以应设甲种货车和乙种货车的载重量为未知数.本题中的等量关系为:2辆甲车的载重量+3辆乙车的载重量=15.5,5辆甲车的载重量+6辆乙车的载重量=35.
解答 解:甲种货车能运x吨,乙种货车能运y吨.
则$\left\{\begin{array}{l}{2x+3y=15.5}\\{5x+6y=35}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=4}\\{y=2.5}\end{array}\right.$,
3x+5y=24.5(吨)
答:这批货物有24.5吨.
点评 本题考查二元一次方程组在表格中的应用,读懂表格,找到相应的等量关系是关键.在本题还需注意是不能设直接未知数的.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
9.如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心,菱形ABCD在直线L上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫做一次操作,则经过2013次这样的操作菱形中心O所经过的路径总长为( )
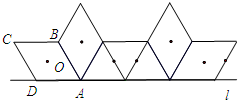

| A. | $\frac{{671(\sqrt{3}+1)}}{3}$π | B. | $\frac{{671(2\sqrt{3}+1)}}{2}$π | C. | $\frac{{671(2\sqrt{3}+1)}}{3}$π | D. | $\frac{{1342\sqrt{3}}}{3}$π |
19.以下生活现象中,属于旋转变换得是( )
| A. | 钟表的指针和钟摆的运动 | B. | 站在电梯上的人的运动 | ||
| C. | 坐在火车上睡觉 | D. | 地下水位线逐年下降 |
4.已知a=3+$\sqrt{5}$,b=3-$\sqrt{5}$,则代数式$\sqrt{{a^2}-ab+{b^2}}$的值是( )
| A. | 24 | B. | ±2$\sqrt{6}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{5}$ |
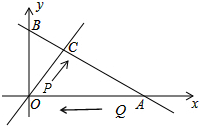 如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.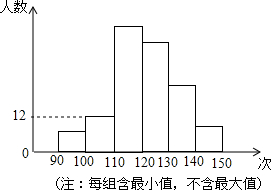 九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题
九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题